Büchi Automaton

Büchi automaton is a type of ω-automaton (omega automaton) that accepts infinite strings. Named after its creator, Julius Richard Büchi, this automaton is fundamental to many areas in formal verification, especially in the realm of model checking for linear temporal logic properties.

---

Contents

---

• Introduction of Büchi Automaton
  • What is Büchi Automaton?
  • Formal Definition
  • Applications
• Finite Automaton
  • Example of Finite Automaton
  • Consists of Finite Automaton
• Büchi Automaton
  • the Difference Between Finite Automaton and Büchi automaton
  • Some Properties of Büchi Automata
  • Example of Büchi Automata

---

Introduction of Büchi Automaton

What is Büchi Automaton?

A Büchi automaton is essentially a nondeterministic finite automaton (NFA) extended to infinite input sequences. Just like an NFA, a Büchi automaton has a finite set of states and transitions. However, the acceptance condition is different, given that the input strings are infinite.

Formal Definition

A Büchi automaton is defined as a tuple ( A = (Q, Σ, δ, q0, F) ), where:

• Q is a finite set of states.
• Σ is a finite input alphabet.
• δ is a transition relation.
• q0 is the initial state.
• F is a set of accepting states.

The acceptance condition for a Büchi automaton is slightly different from the usual finite automata. An infinite word is accepted if there exists a run (a sequence of state transitions) such that the automaton visits one of its accepting states infinitely often.

Applications

Büchi automata are widely used in the formal verification of systems, especially in model checking of linear temporal logic (LTL) properties. LTL is a type of temporal logic that allows statements about sequences of states that a system can take. By converting LTL formulas to Büchi automata, verification tools can then check if a given system (modeled as another type of automaton) satisfies the desired properties.

Finite Automaton

• finite automata accept/reject strings over a given alphabet
• equivalent to regular expressions

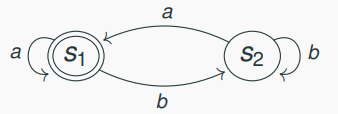
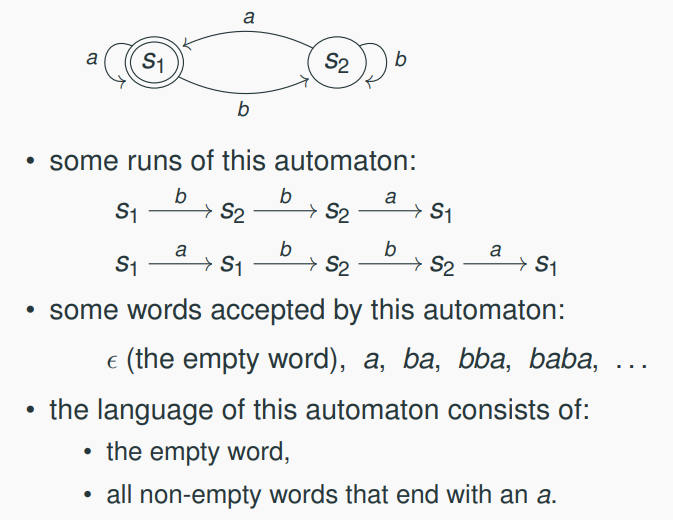
Example of Finite Automaton

• the initial state is s1
• the final state is s1
• the string abba is accepted
• the string bab is rejected

Consists of Finite Automaton

Let Σ be a finite alphabet (consisting symbols that we will use in strings/words over Σ).

• A finite automaton A accepts a finite word a1 … an if there exists a run of A on a1,…, an which ends in an accepting state.

• The language of a finite automaton A, denoted L(A), consists of all the words it accepts.

Büchi Automaton

the Difference Between Finite Automaton and Büchi automaton

1. Input Length:
   • Finite Automaton (FA): It operates on finite-length input strings. This means that the input strings will eventually terminate after a certain number of symbols.
   • Büchi Automaton: It is designed to operate on infinite-length input strings. These strings never terminate and continue indefinitely.
2. Acceptance Condition:
   • Finite Automaton (FA): Acceptance is determined by whether the automaton ends up in a designated “accept” or “final” state after processing the entire input string.
   • Büchi Automaton: Given the infinite nature of the input, acceptance is defined in terms of recurring behaviors. Specifically, an input is accepted if there exists a run (sequence of transitions) such that the automaton visits one of its “accept” or “final” states infinitely often.
3. Usage and Application:
   • Finite Automaton (FA): They are fundamental to many areas in computer science, including lexical analysis (part of the compilation process), pattern matching, and various string-processing algorithms.
   • Büchi Automaton: It’s specifically used in the realm of model checking, especially for checking properties described by linear temporal logic (LTL) over infinite traces or behaviors.

Some Properties of Büchi Automata

Example of Büchi Automata