B+ Tree: How is Indexing of Databases Implemented?

Contents

Introduction to B+ Tree
Why Use B+ tree for Database Indexing?
- Features of Database Indexing
- Can We Use Other Data Structures?
Indexing of Databases: From Binary Search Tree to B+ Tree

Introduction to B+ Tree

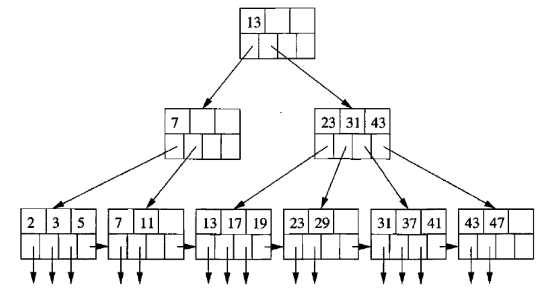
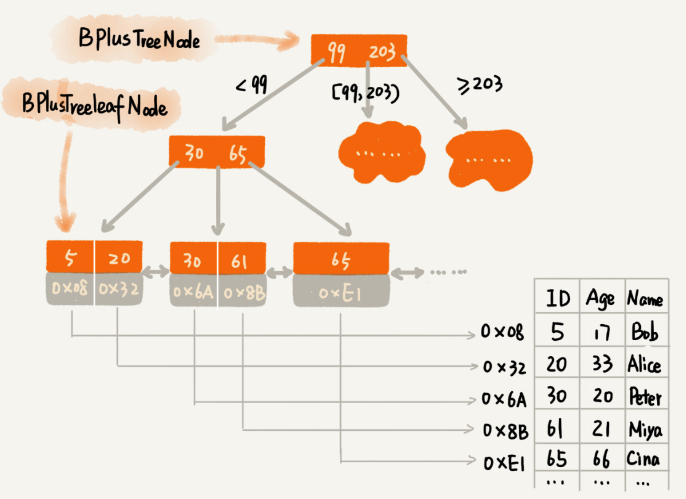
A B+ Tree is a type of self-balancing tree data structure that maintains sorted data and allows searches, sequential access, insertions, and deletions in logarithmic time. It is an extension of the B-Tree, enhancing it with optimized leaf nodes for sequential traversal.

In the realm of database management and file systems, the B+ Tree stands out as a highly efficient data structure for storing and managing large blocks of sorted data.

Structure of B+ Trees

Nodes: B+ Trees consist of internal nodes and leaf nodes. Internal nodes direct the search and do not store actual data records but keys that act as separators directing queries to the correct leaf nodes.
Leaf Nodes: These nodes contain the actual data entries and are linked sequentially, facilitating efficient range queries and sequential access.
Root Node: The top node from which the search begins, potentially spanning multiple levels down to the leaves.

Key Features

High Fan-out: Each node in a B+ Tree contains a large number of children, which reduces the tree’s height and the number of disk I/O operations required.
Leaf Node Linkages: Leaf nodes of B+ Trees are linked, providing an ordered linked list of the entries for quick traversal of all records.
Balance: Every path from the root to a leaf node is of the same length, ensuring that operations remain balanced and efficient.

Advantages of B+ Trees in Database

Efficiency in Range Queries: The linked leaves allow for fast and efficient range queries, which are common in database operations.
Minimized Disk I/O: High fan-out reduces the depth of the tree, thus reducing the disk reads required during operations.
Optimized for Storage Systems: B+ Trees are designed to match the block size of physical disks, maximizing the use of disk space and reducing overhead.

Why Use B+ tree for Database Indexing?

Nowadays, many database engines choose B+ Tree for data indexing. But why?

Features of Database Indexing

The main reason for this is due to the features of database indexing itself.

For database searches, we can categorise frequently perform operations into these two categories:
1. Search for data based on a value. For example, select name from user where id=1234
2. Search for data based on range values. For example, select name from user where id > 1234 and id < 2345
For performance requirements, we mainly consider both time and space, i.e. execution efficiency and storage space.
- For execution efficiency, we want the index to search the data as efficiently as possible;
- For storage space, we want the index not to consume too much memory space.

Can We Use Other Data Structures?

For fast search, insertion, deletion, we can also use hash tables, balanced binary search trees, and skip lists.

But for database indexes, they all have their own limitations:

Hash tables:
- Lack of ordering: Hash tables do not maintain any ordering among keys, which can be a limitation in certain applications where ordered traversal is required.
- Not suitable for range searches: Hash tables are not optimized for range queries, as they rely on exact key matches for retrieval.
- Hash collisions: If multiple keys hash to the same index (a collision), additional operations are needed to handle these collisions, which can degrade performance.
Balanced binary search trees:
- Uncontrollable tree height: If the amount of data is large or the inserted data has a specific distribution, it will lead to an increase in the height of the tree, which will affect the performance of the search.
- Not suitable for range searches: While balanced binary search trees support efficient searching for individual keys, they are not inherently optimized for range queries (e.g., finding all keys within a certain range).
Skip lists:
- Not suitable for persistence: Skip list implementations are relatively complex, especially when persistent storage is required. Since the structure of a skip list relies on randomness, more work is required to ensure proper persistence on disk.
- Uncertain Performance: The performance of skip lists depends heavily on the randomness in their structure. Although skip lists have a good performance in the average case, in the worst case its performance may degrade to O(n), which is unacceptable.

In fact, the B+ tree used for database indexing is very similar to a skip list (non-leaf nodes only store indexes and don’t store data). However, the B+ tree evolved from a binary search tree, not a skip list.

Indexing of Databases: From Binary Search Tree to B+ Tree

To restore the whole process of inventing the B+ tree, we start with a binary search tree and see how it is transformed into a B+ tree step by step based on requirements.

Connecting Leaf Nodes Using a Linked List for Range Searches

As I said before, Binary Search Tree is not suitable for range search. So that’s the first problem we have to solve.

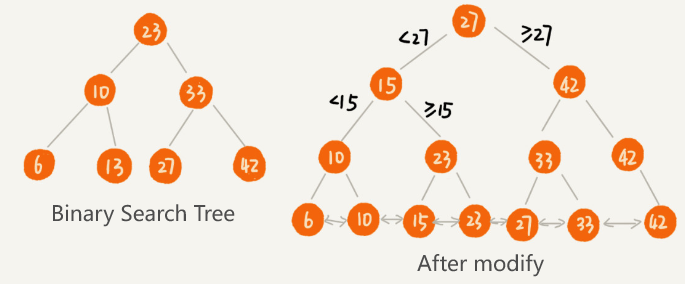
To make a binary search tree better support searching data by range, we can modify it like this:
- The nodes in the tree do not store the data itself, but rather just serve as indexes.
- Each leaf node is linked on a linked list, and the data in the linked list is ordered from smallest to largest.

The modified binary tree looks like a skip list:

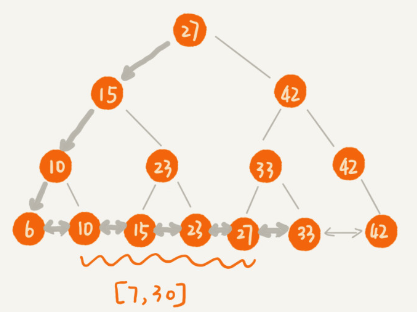
After the transformation, if we require data in a certain range:
- We just need to do a search in the tree to find the first leaf node that satisfies the range.
- Then traverse back down the link list until the value of the node data in the link list is greater than the termination value of the range.

search data in [7, 30]

But this causes another problem:

Need extra space to store index nodes.

Using Disk for Storing Large Amounts of Indexes

We also need to consider scenarios where the amount of data is too large.
- For example, if we build a binary search tree index for a table with 100 million of data, the index will contain about 100 million nodes. Assuming 16 bytes per node, that’s about 1GB of memory space.
- If we were to index 10 tables or even more, the memory requirements would be insatiable.

How can we solve this problem of the index taking up too much memory?

We can store the index on the disk.

But this causes another problem:

Disk IO is very time-consuming compared to memory reads and writes. So the focus of our optimisation is to minimise disk IO operations.

Minimise Tree Height for Reducing Disk IO

If the tree is stored on the disk, then each read (or access) to a node corresponds to a disk IO operation.

The height of the tree is equal to the number of disk IO operations for each data query.
So we need to minimise the height of the tree

How to reduce the height of the tree?

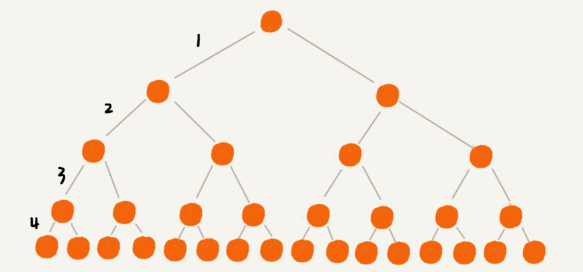
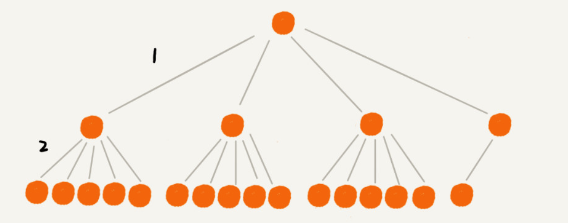
We can build the index as an m-way tree (m > 2).

binary tree

5-way tree

From the above figure, it can be seen that storing the same number of nodes, the m-way tree (m > 2) has a lower height than the binary tree.
- The larger the m in the m-way tree, the smaller the height of the m-way tree.
- So what’s the best value for m?

No matter the data in memory or on the disk, the operating system reads the data on a page-by-page basis:
- The size of a page is usually 4KB, and this value can be viewed with the getconfig PAGE_SIZE command.
- The data will be read one page at a time.
- If the amount of data to be read exceeds the size of one page, multiple IO operations will be triggered.
Therefore, we should try to make the size of each node (m size) equal to the size of a page:
- Reading a node requires only one disk IO operation.
- Whilst minimise the height of the tree.

Maintain the Size of Each Node

In order to minimise IO, the m-value (size of each node) of the B+ tree is pre-calculated based on the size of the page, i.e. each node can have at most m children.

With the increase of data in the database, it is possible for some nodes to have more than m children. In this case, the size of the node exceeds the size of a page, and reading such a node results in multiple disk IO operations.

How to solve the problem of a B+ tree with the node size greater than m?
- It’s very simple. We just need to split this node into two nodes.
  - However, after the node is split, it is possible that its parent node has more than m children. But it doesn’t matter. We can use the same method to split the parent node into two nodes as well. This cascading reaction works from the bottom up to the root node.
- Similarly, when we delete data, we may also need to update the index nodes. Frequent data deletion results in the number of children of some nodes becoming very small. This can lead to less efficient indexing.
  - For example, we can merge nodes which are too small.

So, Insertion in a B+ Tree follows these steps:

Finding the Correct Leaf Node: Start from the root and traverse down to find the appropriate leaf node where the new key should be inserted.
Inserting in the Leaf Node: Insert the new key in the sorted order of keys in the leaf node.
Splitting: If the leaf node overflows (i.e., exceeds the maximum number of entries it can hold), it is split into two, and the median is pushed up to the parent node. This may cause a recursive split up the tree if the parent node also overflows.

Deletion involves removing an entry from the leaf node and then possibly adjusting the tree structure to maintain balance:

Leaf Node Adjustment: After deletion, if a leaf node underflows (i.e., has fewer entries than the minimum required), it may borrow an entry from a sibling node or merge with a sibling.
Propagation Upwards: If a merge occurs, it may reduce the number of entries in the parent node, possibly leading to further merging or adjustments up the tree.

This is why adding indexes, while making searching data more efficient, also makes writing data less efficient:

The process of writing data will involve index updates. The more indexes there are, the more updates are involved.

So in practice, in order to ensure the overall efficiency of database operations, we only build indexes for the necessary attributes.

In addition to the B+ tree, you may have heard of the B tree (or B-tree). The B tree is actually a Simplified version of the B+ tree. Their main differences are:

Nodes in the B+ tree store indexes, while nodes in the B tree store data.

The leaf nodes in a B tree do not need a linked list to be chained together.

This leads to B tree being unsuitable for common database operations such as sorting, range searching, and traversal.

This means that the B-tree is more like a normal self-balancing m-way tree.

Reference:

Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.
Introduction of B-tree (2023) GeeksforGeeks. Available at: https://www.geeksforgeeks.org/introduction-of-b-tree-2/
https://dba.stackexchange.com/questions/155945/b-tree-structure-with-buckets-begginer-question