What is a Backtracking Algorithm?
A backtracking algorithm tries to build a solution to a problem incrementally. If the current partial solution is not valid, the algorithm discards it and backtracks to the previous step, trying a different path. This process continues until a valid solution is found or all possibilities have been exhausted.
Key Principles
- Incremental Construction: Build the solution step-by-step.
- Validation: Check if the current partial solution is valid.
- Backtracking: If the current solution is invalid, revert to the previous step and try a different path (like Pruning in Brute Force).
The backtracking algorithm is actually very simple, which is
Brute Force + Pruning: traverse all the cases (Brute Force) and stop traversing and back to the previous path when a path does not satisfy the conditions (Pruning).
- When using the backtracking algorithm, we enumerate all the solutions and find those that satisfy the expectation.
- We divide the problem into multiple stages. At each stage, we face a fork in the road, we pick a path to go down, and when we find that this path doesn’t work (doesn’t satisfy the conditions), we backtrack to the previous fork in the road and pick the next path to go down.
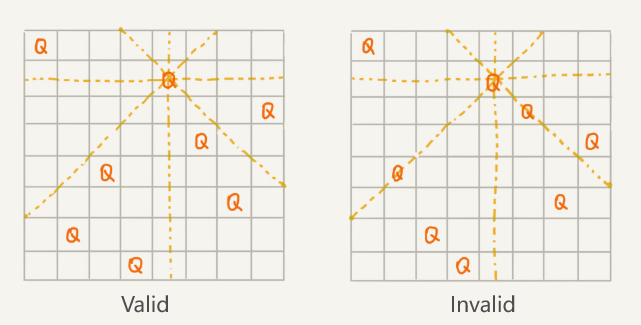
Backtracking algorithms are usually suitable for search-solution scenarios where the regularity is not known (e.g., the Eight Queens problem).
- Because we don’t know the regularity of these scenarios, we have to traverse all the solutions.
- However, when we encounter a step that does not satisfy the condition, we should backtrack to the previous step to avoid useless calculations.
For problems with regularity, of course, we can also use backtracking to solve them. But this is not suitable because we can take a more efficient approach. For problems with regularity, we don’t need to solve it by brute force, and we can reduce some unnecessary computations by regularity (e.g., by using dynamic programming).
Advantages of Backtracking
- Flexibility: Can be applied to a wide range of problems, especially combinatorial and constraint satisfaction problems.
- Simplicity: Straightforward to implement and understand.
- Optimality: Guarantees finding an optimal solution if one exists, as it explores all possibilities.
Disadvantages of Backtracking
- Inefficiency: Can be slow for large problems due to its exhaustive search nature.
- High-Time Complexity: Time complexity can grow exponentially with the size of the input.
Applications of Backtracking Algorithms
Backtracking algorithms are used in various fields to solve complex problems, including:
- Puzzle Solving: Sudoku, N-Queens problem, crossword puzzles.
- Combinatorial Problems: Generating permutations, combinations, and subsets.
- Constraint Satisfaction Problems: Graph coloring, scheduling problems.
- Pathfinding: Maze solving, robot navigation.
Example 1: N-Queens Problem
The N-Queens problem involves placing N queens on an N×N chessboard so that no two queens threaten each other. This means no two queens share the same row, column, or diagonal.
This is a hard problem from Leetcode: 51. N-Queens. And many people always feel this question is hard too. But actually, it is very simple to solve this problem with backtracking and recursion.
Steps
- Place: Place a queen in the first row.
- Validate: Check if the placement is safe (no two queens share the same row, column, or diagonal).
- Backtrack: If unsafe, move the queen to the next column (for loop) in the same row and check again. If all columns are unsafe, backtrack to the previous row (only safe columns will go to the next recursion).
Implementation in Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
private int n;
private int[] records;
private final List<List<String>> result = new ArrayList<>();
public List<List<String>> solveNQueens(int num) {
n = num;
records = new int[n];
calNQueens(0);
return result;
}
private void calNQueens(int row) {
if (row == n) {
addToResult(records);
return;
}
for (int column = 0; column < n; column++) { // Brute Force solution: a for loop nesting a recursive function
if (isSafe(row, column)) { // Pruning for above Brute Force: For unsatisfied cases, do not continue the recursion
records[row] = column;
calNQueens(row + 1);
}
}
}
private boolean isSafe(int row, int column) {
int leftup = column - 1, rightup = column + 1;
for (int i = row - 1; i >= 0; i--, leftup--, rightup++) { // check each row above
if (records[i] == column) { // Is there a queen directly above?
return false;
}
if (leftup >= 0 && records[i] == leftup) { // Is there a queen on the left upper diagonal?
return false;
}
if (rightup < n && records[i] == rightup) { // Is there a queen on the right upper diagonal?
return false;
}
}
return true;
}
private void addToResult(int[] records) {
List<String> tempStr = new ArrayList<>();
for (int row = 0; row < n; ++row) {
char[] temp = new char[n];
for (int column = 0; column < n; ++column) {
if (records[row] == column) {
temp[column] = 'Q';
} else {
temp[column] = '.';
}
}
tempStr.add(String.valueOf(temp));
}
this.result.add(tempStr);
}
The above code may look like a lot, but there are actually only two important functions: calNQueens() and isSafe() (solveNQueens() is used to initialise member variables and addToResult() adds this valid record to the returned result).
calNQueens(): This function uses recursion, which may seem difficult to understand, but is actually very simple. Here, the for loop and recursion are actually equivalent to two levels of iteration: enumerating all possible outcomes based onrowandcolumn.isSafe(): This function is even simpler, determining if the location is safe based onrowandcolumn.
So, you see, using backtracking, the apparently complex N-Queen problem has been solved so simply!
Example 2: 0/1 Knapsack
The 0/1 Knapsack problem involves selecting items with given weights and values to maximize the total value without exceeding the weight capacity of the knapsack. Each item can either be included in the knapsack (1) or not included (0), hence the name 0/1 Knapsack.
Problem Statement
Given:
nitems, each with a weightw[i]and a valuev[i]- A knapsack with a maximum weight capacity
W
Find:
- The maximum total value that can be obtained without exceeding the weight capacity
W
Steps
The classic solution to the 0/1 Knapsack problem is dynamic programming. However, we can solve this problem using backtracking algorithms. This would be very simple, but not efficient (time complexity is exponential: O(2^n)):
- We can arrange the
nitems in order, and the whole problem is broken down intonstages. - Each stage corresponds to how an item is chosen (two choices: pack it in, or don’t pack it in).
- Just process all items recursively.
- Start: Begin with an empty knapsack and zero value.
- Include/Exclude: For each item, recursively include it in the knapsack (if it does not exceed the capacity) or exclude it.
- Update Value: Keep track of the maximum value.
Implementation in Java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private static int maxValue = 0; // To store the maximum profit
// Begin with: knapsack(weights, values, capacity, 0, 0, 0);
public static void knapsack(int[] weights, int[] values, int capacity, int index, int currentWeight, int currentValue) {
if (index == weights.length) {
if (currentValue > maxValue) {
maxValue = currentValue;
}
return;
}
knapsack(weights, values, capacity, index + 1, currentWeight, currentValue); // don't pack it in
if (currentWeight + weights[index] <= capacity) { // Pruning: If the capacity has been exceeded, do not pack it.
knapsack(weights, values, capacity, index + 1, currentWeight + weights[index], currentValue + values[index]); // pack it in
}
}
Reference:
- Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.