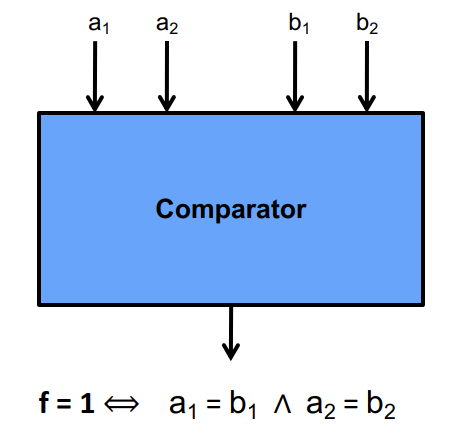
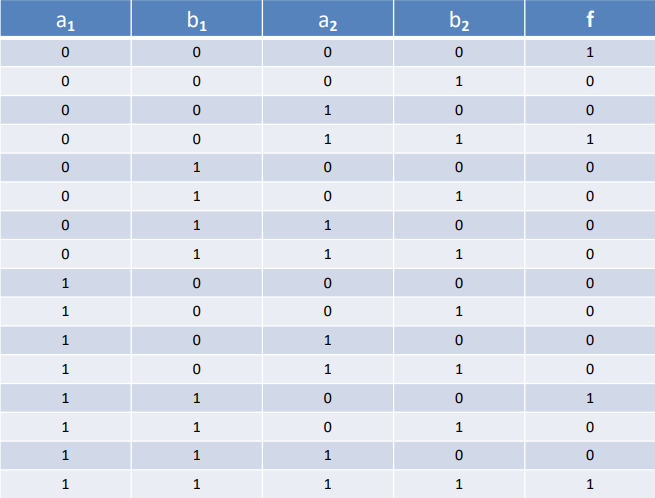
Binary Decision Diagrams (BDDs) are a data structure that is pivotal in the realms of computer science and engineering, especially for representing Boolean functions.
one of the only really fundamental data structures that came out in the last twenty-five years
—— Donald Knuth, Fun with Binary Decision Diagrams, 2008 lecture
- What are Binary Decision Diagrams?
- Importance of BDDs
- Applications of BDDs
- How to get a ROBDD of Comparator?
- Variable Ordering of ROBDDs
- Logical Operations on ROBDDs
- Some Limitations in Working with ROBDDs
What are Binary Decision Diagrams?
Binary Decision Diagrams are a form of data structure used to represent and manipulate Boolean functions efficiently. A BDD is a rooted, directed acyclic graph that comprises several decision nodes and terminal nodes.
The Structure of BDDs
- Decision Nodes: These nodes represent the variables of the function. Each decision node has two child nodes corresponding to the two possible values (true or false) of the variable.
- Terminal Nodes: These nodes represent the function’s output and are typically labeled ‘0’ or ‘1’.
Reduced Ordered Binary Decision Diagrams (ROBDDs)
An important subclass of BDDs is Reduced Ordered Binary Decision Diagrams (ROBDDs). It is ordered because variables are arranged in a specific sequence, and it is reduced by merging identical subgraphs and eliminating redundant nodes. ROBDDs are deterministic, meaning the same function will always result in the same diagram. They are efficient for logical operations and are commonly used in digital circuit design and formal verification. However, the size of a ROBDD is dependent on the variable ordering, and finding the optimal order is a complex task.
Importance of BDDs
Efficient Representation
BDDs can represent complex Boolean expressions compactly, often much more so than truth tables or normal forms.
Facilitating Operations
Operations like conjunction, disjunction, and negation on Boolean functions are more efficient and easier to perform using BDDs.
Canonical Form
In the case of OBDDs, the canonical form ensures uniqueness, making them ideal for equivalence checking.
Applications of BDDs
- Model Checking
- BDDs are extensively used in model checking, specifically in symbolic model checking, for representing state spaces of systems efficiently.
- Circuit Design and Verification
- In hardware design, BDDs are used for circuit verification and synthesis. They help in optimizing circuit layouts and checking the equivalence of circuits.
- Boolean Function Manipulation
- BDDs are ideal for applications involving complex Boolean function manipulations, such as those found in artificial intelligence and computational logic.
How to get a ROBDD of Comparator?
OBDT Example of Comparator
Comparator
Truth Table
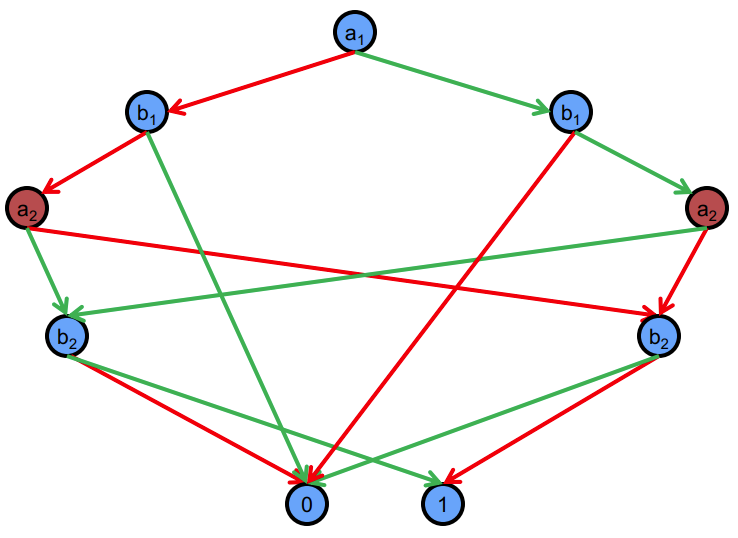
Binary Decision Tree (red line is 0, green line is 1)
Binary Decision Tree (BDT):
- Length of each path = number of variables
- Leaf nodes labelled with either 0 or 1
- Every node on a path labelled with a different variable
- Internal node v has two children: low(v) and high(v)
- Assign 0 to var(v) if low(v) is in the path, and 1 if high(v) is in the path
- Looking up the truth table with this truth assignment
- A BDT is ordered if the variables appear in the same order along each path
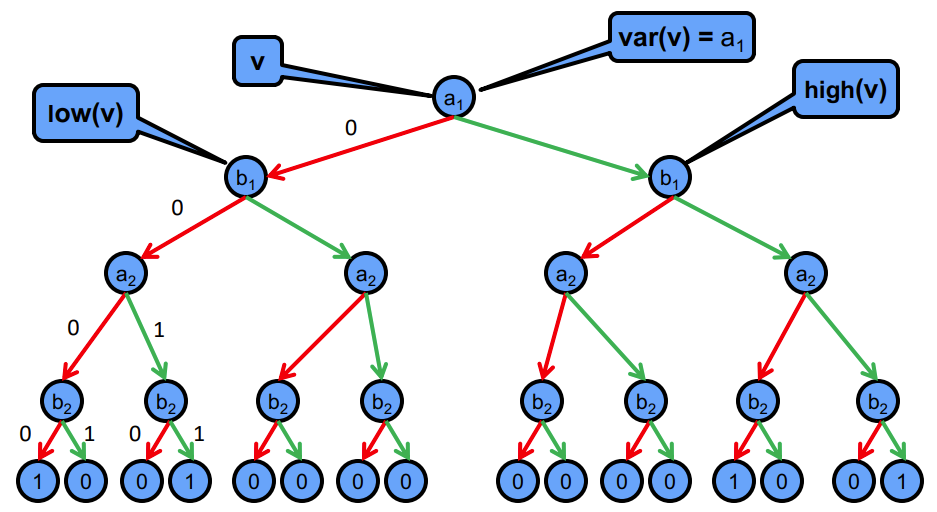
OBDT to ROBDD
- Conceptually, a ROBDD is obtained from an ordered BDT(OBDT) by eliminating redundant nodes/sub-diagrams
- ROBDD is often exponentially smaller than the corresponding OBDT
- Start with OBDT and repeatedly apply the following three operations as long as possible:
- Merge equivalent leaves.
- Eliminate redundant tests. Whenever
low(v) = high(v), removevand redirect edges intovtolow(v).- Merge isomorphic nodes.
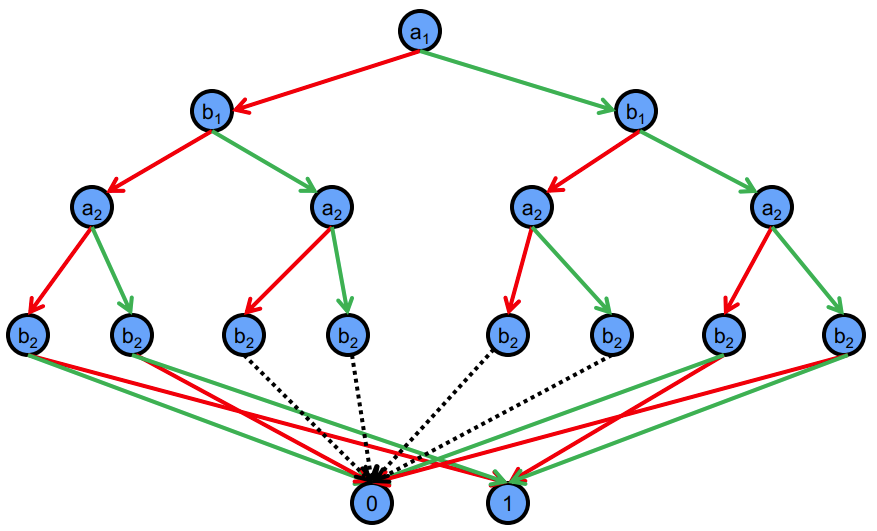
Merging equivalent leaves (0 and 1) of the above Binary Decision Tree, and we get the diagram below:
Merge equivalent leaves
The above diagram is the result of merging equivalent leaves. And The dotted lines in the diagram indicate redundant tests, where low(v) = high(v). We can eliminate them and get the diagram below:
Eliminate redundant tests
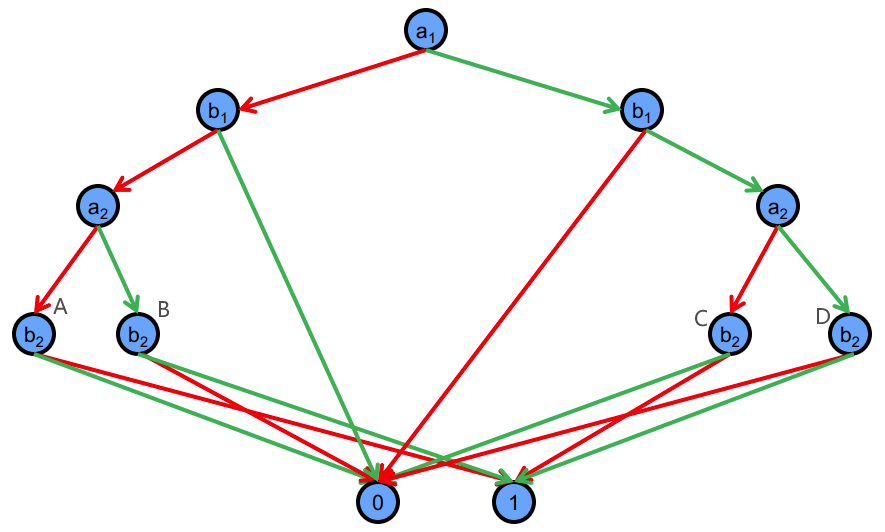
The above diagram is the result of eliminating redundant tests. And A and C in the diagram are isomorphic, and B and D are also isomorphic. We can merge it get the diagram below:
Merge isomorphic nodes
The above diagram still contains isomorphic nodes (two red nodes). We can merge it get the diagram below (we move the b2 node so that the BDD looks nicer):
Keep merging isomorphic nodes
Variable Ordering of ROBDDs
The size of a ROBDD is dependent on the variable ordering.
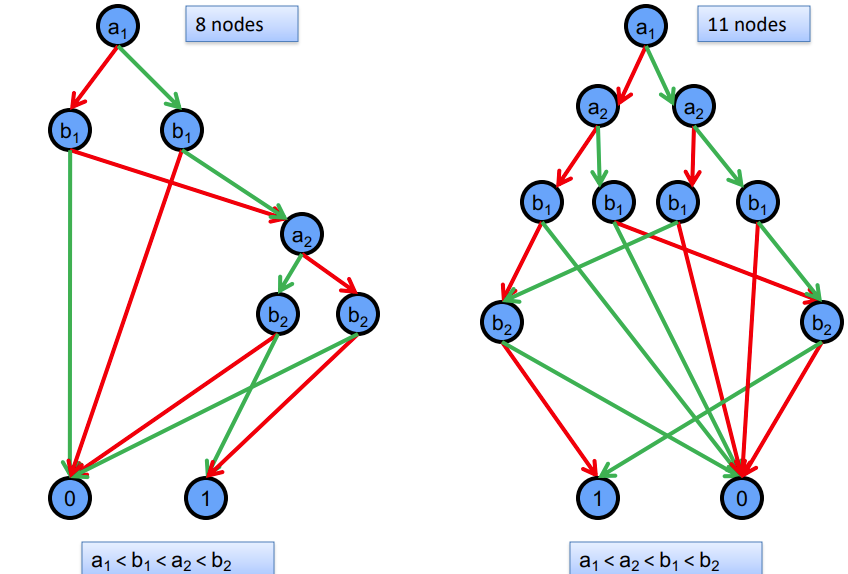
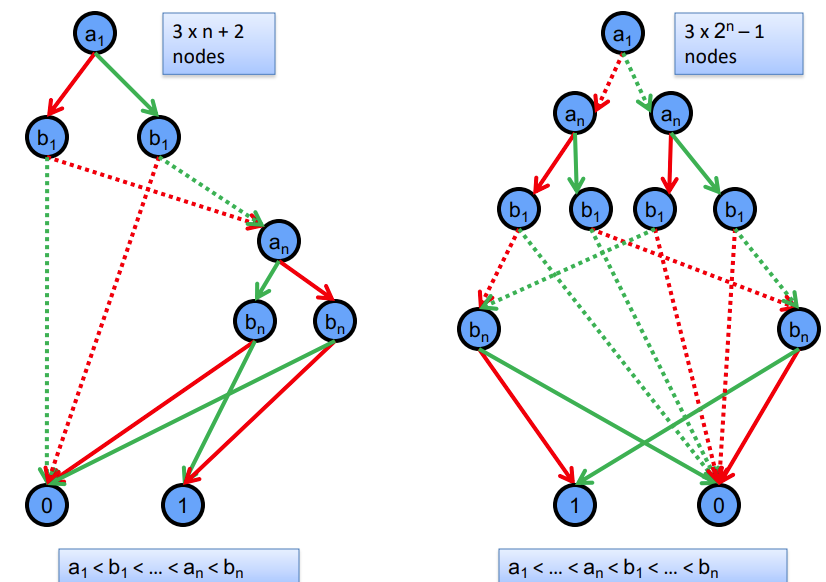
There are Boolean functions that have exponential size OBDDs for any variable ordering.
Logical Operations on ROBDDs
ROBDD Operations
Some Limitations in Working with ROBDDs
- they can often become large
- variable ordering must be uniform along paths
- selecting the “right” variable ordering is crucial
- in some cases, no space-efficient variable ordering exists
