Bounded Model Checking

---

Contents

---

• What is Bounded Model Checking? Why bounded?
  • Model Checking versus Bounded Model Checking
  • Bounded Model Checking for Reachability
• Example: Two Bit Counter
• CBMC: How Does It Work?
  • Control Flow Simplification
  • Loop Unwinding
    • Example
  • Transforming Loop-Free Programs Into Equations
    • Static Single Assignment
    • Example 1
    • Example 2 (with a Loop)

---

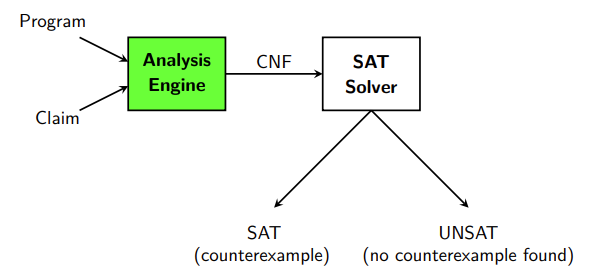
What is Bounded Model Checking? Why bounded?

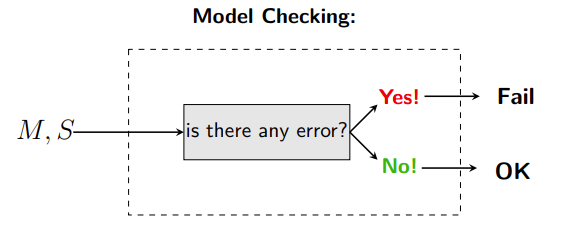
• Model Checking is supposed to be exhaustive, i.e. the whole state space of the system is explored.
• In real world systems, the number of states is usually too big (state space explosion problem).
• We can explore only a subset of the state space: Bounded Model Checking (BMC)

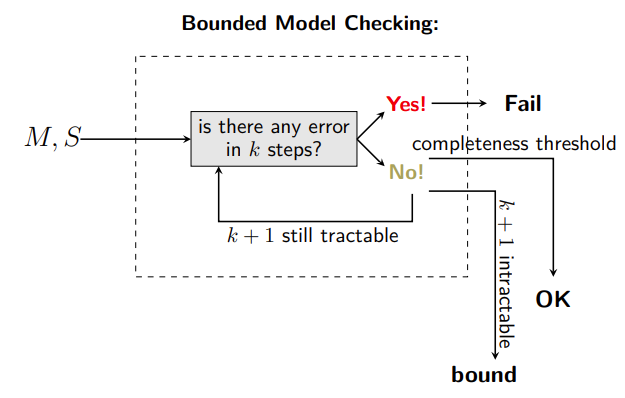
Model Checking versus Bounded Model Checking

BMC: check if a property holds for a subset of states

Bounded Model Checking for Reachability

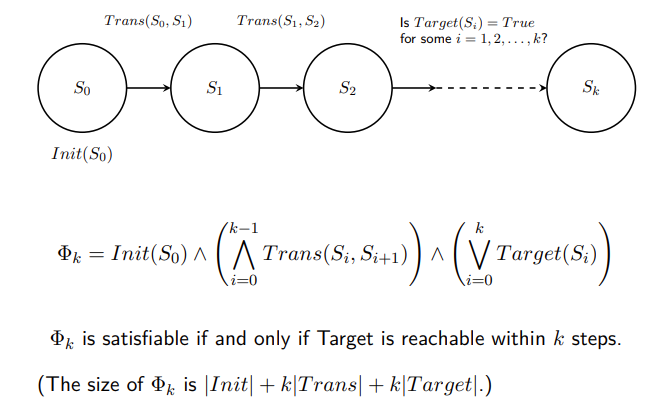
• Given a positive integer k, is the Target reachable in k steps? (Think of Target as defining bad states.)
• We encode a BMC problem as a SAT problem.
• The Bounded Model Checking problem X, Init(X), T arget(X), T rans(X, X′), k, is transformed into a Boolean formula Φk.
• Φk is satisfiable iff(if and only if) Target is reachable from Init within k steps following Trans.

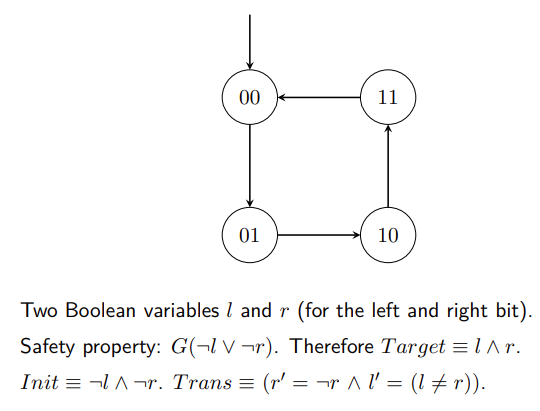
Example: Two Bit Counter

encode a BMC problem as a SAT problem

• Φ2 is unsatisfiable (hence, no proof of violation of the safety property).
• Φ3 (l3 = 1, r3 = 1) is satisfiable (so the safety property is violated).

---

Main idea: Given a program and a claim, use a SAT solver to check of there is an execution that violates the claim.

CNF stands for Conjunctive Normal Form. It is a way of structuring logical expressions in a form where a series of AND operations (conjunctions) are applied to OR expressions (disjunctions) of literals. A literal is either a variable or the negation of a variable.

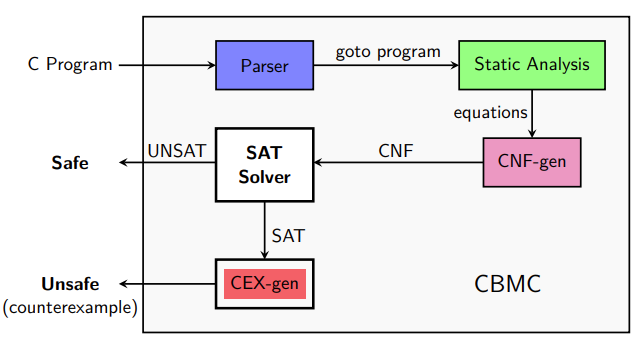
CBMC: How Does It Work?

CBMC: the C (Program) Bounded Model Checker

---

Transforms a C program into a set of equations:

1. Simplify control flow
2. Unwind all the loops
3. Convert into Single Static Assignment (SSA)
4. Convert into equations
5. Bit-blast
6. Solve with a SAT solver
7. Convert SAT assignment into a counterexample

Control Flow Simplification

• All side effects are removed
  • e.g. j=i++; is transformed into j=i; i=i+1;
• Control flow is made explicit
  • continue and break are replaced by goto
• All loops are simplified into one form
  • e.g. for, do, while are replaced by just while

Loop Unwinding

• All loops are unwound
  • use different unwinding bounds for different loops
  • check whether unwinding is sufficient using a special unwinding assertion
• If a program satisfies all of its claims and all unwinding assertions, then it is correct.
• Recursive functions and backward goto are similar (use inlining).

void f(...) {
    ... // some code
    while(cond){
        Body;
    }
    Remainder;
}

• while loops are unwound iteratively;
• break/continue replaced by goto.

void f(...) {
    ... // some code
    if (cond) {
        Body;
        if (cond) {
            Body;
            if (cond) {
                Body;
                while (cond) {
                    Body;
                }
            }
        }
    }
    Remainder;
}

• Assertion inserted after last iteration: violated if the program runs longer than bound permits. Positive correctness result!

void f(...) {
    ... // some code
    if (cond) {
        Body;
        if (cond) {
            Body;
            if (cond) {
                Body;
                assert (!cond); //Unwinding assertion
            }
        }
    }
    Remainder;
}

Example

Sufficient Loop Unwinding

Insufficient Loop Unwinding

Transforming Loop-Free Programs Into Equations

It is trivial to translate a program into a set of equations if each variable is only assigned once!

x = a;
y = x+1;
z = y-1;

This program is directly transformed into: x = a ∧ y = x + 1 ∧ z = y − 1

Static Single Assignment

Static Single Assignment (SSA) form:

• Every variable is assigned exactly once.
• Every variable is defined before it is used.

---

x=x+y; 
x=x*2;
a[i]=100;

When a variable is assigned multiple times, we use a new variable for each assignment:

x1 = x0 + y0;
x2 = x1*2;
a1[i0] = 100;

---

if(v)
    x = y;
else
    x = z;
w = x;

Converting conditionals to SSA:

if(v0)
    x0 = y0;
else
    x1 = z0;
x2 = v0 ? x0 : x1;
w1 = x2;

Example 1

int y;
int x;
x = x + y;
if (x != 1)
    x = 2;
else
    x++;
assert (x <= 3);

Convert to SSA (Static Single Assignment form):

x1 = x0 + y0;
if (x1 != 1)
    x2 = 2;
else
    x3 = x1 + 1;
x4 = (x1 != 1) ? x2 : x3;
assert (x4 <= 3);

Generate constraints (if SAT, then assertion is false):

x1 = x0 + y0 ∧ x2 = 2 ∧ x3 = x1 + 1

∧ ((x1 ≠ 1 ∧ x4 = x2) ∨ (x1 = 1 ∧ x4 = x3)) [selector]

∧ ¬(x4 ≤ 3) [negated assertion]

Example 2 (with a Loop)

int i;
int p;
p=5;
for (i=0; i<=n; i++) {
    p = p * m;
}
assert(p>=5);

Transform the for loop into a while loop:

int i;
int p;
p = 5; i = 0;
while (i <= n) {
    p = p * m;
    i = i + 1;
}
assert(p >= 5);

Unroll the loop twice and add an assume statement to exit the loop:

int i;
int p;
p = 5; i = 0;
if (i <= n) {
    p = p * m;
    i = i + 1;
    if (i <= n) {
        p = p * m;
        i = i + 1;
        assume(!(i <= n));
    }
}
assert(p >= 5);

Assign all variables exactly once, compute guards for conditionals and add conditionals for merging values:

p1 = 5; 
i1 = 0;
g1 = i1 <= n1
    p2 = p1 * m1; // g1
    i2 = i1 + 1;  // g1
    g2 = i2 <= n1
        p3 = p2*m1  //g1 && g2
        i3 = i2 + 1;  //g1 && g2
        assume(!(i3 <= n1));
p4 = g1 ? (g2 ? p3 ? p2) : p1;
i4 = g1 ? (g2 ? i3 : i2) : i1;  // i4 unused
assert(p4 >= 5);

Convert to logical expression (if UNSAT, then assertion holds):

p1 = 5

∧ i1 = 0

∧ g1 = (i1 ≤ n1)

∧ p2 = p1 ∗ m1

∧ i2 = i1 + 1

∧ g2 = (i2 ≤ n1)

∧ p3 = p2 ∗ m1

∧ i3 = i2 + 1

∧ ¬(i3 ≤ n1) [assume statement]

∧ p4 = g1 ? (g2 ? p3 : p2) : p1

∧ i4 = g1 ? (g2 ? i3 : i2) : i1

∧ ¬(p4 ≥ 5) [assert statement]