- What is Explicit State Model Checking
- Key Components of Explicit State Model Checking
- Explicit State Model Checking using Automata
- Benefits and Limitations of Explicit State Model Checking
What is Explicit State Model Checking
Explicit State Model Checking is a method used in formal verification where the state space of a system is explicitly enumerated to verify its properties. It involves exploring all possible states and transitions of a system to check for properties like safety, liveness, and deadlock freedom.
Key Components of Explicit State Model Checking
State Space Generation
- The model checker generates the state space of the system by simulating all possible actions from each state.
- This results in a graph where nodes represent states, and edges represent transitions between states.
Property Specification
- Properties to be verified are specified using temporal logics, such as Linear Temporal Logic (LTL) or Computational Tree Logic (CTL).
- These properties define the correct behavior of the system in terms of its states and transitions.
Systematic Exploration
- The model checker systematically explores the state space, checking whether the specified properties hold in each state.
- It uses algorithms to traverse the graph, inspecting each node (state) and its outgoing edges (transitions).
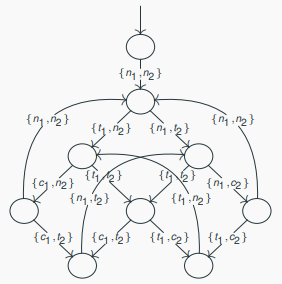
Explicit State Model Checking using Automata
Transition systems can be transformed into Büchi automata (Place Prop in the middle of the line in the opposite direction of the arrow):
- The states of the automaton correspond to states of the transition system, plus one additional initial state.
- There is one transition from the new (and only!) initial state to all the states corresponding to initial states in the transition system.
- All other transitions of the automaton correspond to transitions in the transition system.
- The alphabet of the automaton is the set of all subsets of
Prop, that isP(Prop). (Prop = {n1, n2, t1, t2, c1, c2}) - The labels on automaton transitions are inherited from the target states in the transition system.
- All automaton states are accepting. (So all runs will be accepting!)
Question: What are the words accepted by the resulting automaton?
Answer: Exactly those infinite sequences of sets of atomic propositions that occur along computation paths through the transition system!
For example:
- atomic propositions:
Prop = {n1, n2, t1, t2, c1, c2} {n1, n2} → {t1, n2} → {c1, n2} → {n1, n2} → ...occurs along a path through the transition system- So,
{n1, n2}, {t1, n2}, {c1, n2}, {n1, n2},...is accepted by the automaton
Intuition: runs of the automaton correspond to paths through the transition system.
- LTL formula involving
Propcan also be transformed into an automaton over the alphabetP(Prop).- infinite words over
P(Prop)describe sequences of sets of atomic propositions - the resulting automaton should accept an infinite word precisely when the corresponding sequence satisfies the given formula
- infinite words over
- since the model and the specification are both automata, we can use the theory of Büchi automata to do model-checking!
From LTL to Automata
For example (Mutual Exclusion):
Mutual Exclusion Property: A G ¬(c1 ∧ c2) (c1 and c2 are mutually exclusive)
 From LTL(
From LTL(A G ¬(c1 ∧ c2)) to Automata
The above automaton accepts all infinite words not containing both c1 and c2 at the same time (i.e. within the same “symbol”).
A proper mutual exclusion system must also satisfy the liveness property: A F c1 and A F c2 (critical state c1 and c2 must be reachable)
The above automaton accepts all infinite words eventually containing c1 as part of a “symbol”.
Properties of Automata
Assuming the existence of automaton A and automaton S, and model satisfies the specification L(A) ⊆ L(S), thus:
Use the Properties of Automata to Do Model Checking
We can use the above one of properties of automata to do model checking:
Example 1
Check that the following automata A satisfy mutual exclusivity (A G ¬(c1 ∧ c2)):
negation of mutual exclusion (A G ¬(c1 ∧ c2)) is: A F (c1 ∧ c2)
We assume that the automata of A F (c1 ∧ c2) is B
 From LTL(
From LTL(A F (c1 ∧ c2)) to Automata B
The above automaton means that only c1 ∧ c2 can reach to accepting states(final states). So, product automaton of A ∩ B will be:
 Product automaton of
Product automaton of A ∩ B, no accepting states(final states)
Product automaton has no accepting states, hence does not accept any infinite word.
Since the language accepted by the product automaton (A ∩ B) is empty. L(A ∩ B) = ∅, so, L(A) ∩ L(B) = ∅.
B is the negation of mutual exclusion, Then, according to the properties of automata, L(A) ⊆ mutual exclusion.
So, automata A satisfy mutual exclusivity A G ¬(c1 ∧ c2).
Example 2
Check that the following automata A satisfy liveness property (A F c2):
negation of liveness property (A F c2) is: A G ¬c2
We assume that the automata of A G ¬c2 is B
 From LTL(
From LTL(A G ¬c2) to Automata B
The above automaton means that ¬c2 is global, or c2 can’t exist. So, product automaton of A ∩ B will be:
 Product automaton of
Product automaton of A ∩ B, has accepting states(final states)
Product automaton has accepting states, hence accept some infinite words.
Since the language accepted by the product automaton (A ∩ B) is not empty. L(A ∩ B) ≠ ∅, so, L(A) ∩ L(B) ≠ ∅.
B is the negation of liveness property, Then, according to the properties of automata, L(A) ⊄ liveness property.
So, automata A do not satisfy liveness property A F c2.
Benefits and Limitations of Explicit State Model Checking
The above examples are Explicit State Model Checking.
Explicit State Model Checking:
Explicit State Model Checking is a verification method that explores all possible states of a system to ensure it meets specified properties. It explicitly examines each state, but can be resource-intensive due to the state explosion problem.
Benefits:
- automatic
- exhaustive
- produces counter-examples
Limitations:
- state explosion problem (partially addressed by Symbolic Model Checking)
- only works for finite-state systems





