Graphs are a fundamental data structure in computer science and mathematics, used to model pairwise relations between objects. They are widely applicable in various fields such as network analysis, social media, transportation, and more.
What is a Graph?
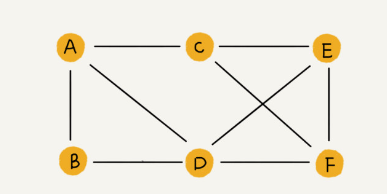
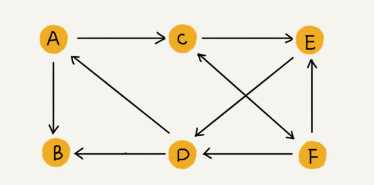
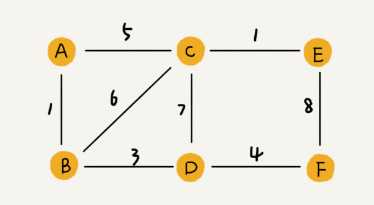
A graph is a collection of nodes, called vertices, and edges that connect pairs of vertices. Formally, a graph is denoted as G(V, E), where V is the set of vertices and E is the set of edges.
Related Concepts
- Vertex (Node): A fundamental part of a graph representing an entity. For example, in a social network graph, vertices represent people.
- Edge (Link): A connection between two vertices representing a relationship. In a social network graph, edges represent friendships.
- Degree: The number of edges connected to a vertex. In a directed graph, each vertex has an in-degree (incoming edges) and out-degree (outgoing edges).
- Path: A sequence of vertices connected by edges.
- Cycle: A path that starts and ends at the same vertex.
- Connected Graph: A graph in which there is a path between every pair of vertices.
- Directed Graph (Digraph): A graph where edges have a direction, indicating the relationship flows from one vertex to another.
- Undirected Graph: A graph where edges do not have a direction.
- Weighted Graph: A graph where each edge has a weight.
How to Represent a Graph
Graphs can be represented in several ways, the most common being the adjacency matrix and the adjacency list. Each representation has its own strengths and weaknesses.
Adjacency Matrix
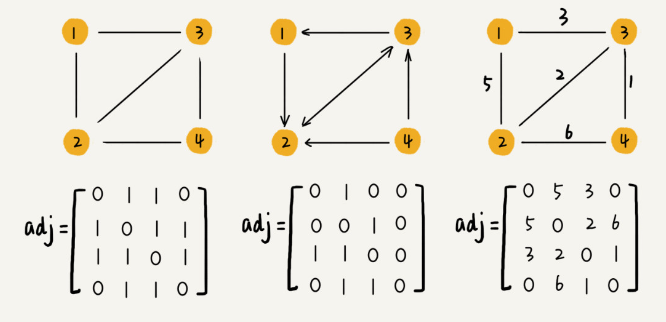
An adjacency matrix is a 2D array of size V^2, where V is the number of vertices in the graph. The element at the i row and j column indicates whether there is an edge from vertex i to vertex j.
- For an undirected graph, if there is an edge between vertex
iand vertexj, we markA[i][j]andA[j][i]as 1; - For a directed graph, we mark
A[i][j]as 1 if there is an edge between vertexiand vertexjwith an arrow pointing fromitoj. - For a weighted graph, the corresponding weights are stored in the array.
Pros and Cons
Pros:
- Quick Edge Look-Up: Checking if an edge exists between two vertices is
O(1). - Simple Implementation: Easy to implement and understand.
Cons:
- Space Inefficiency: Requires
O(V^2)space, which can be prohibitive for large graphs. - Not Suitable for Sparse Graphs: Not suitable for sparse graphs as it wastes a lot of space representing non-existent edges.
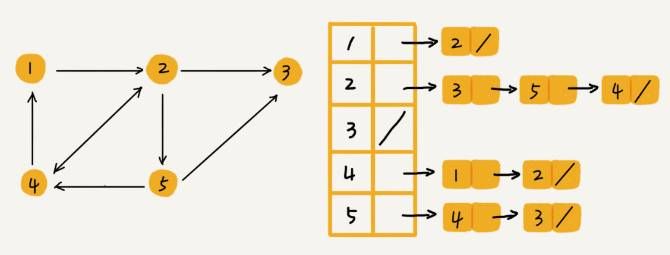
Adjacency List
To address the above problem of wasted memory space in the adjacency matrix, let’s consider another way of storing graphs: the adjacency list.
An adjacency list is an array of lists. The array index represents the vertex, and each element in the list represents the vertices adjacent to that vertex (It’s kind of like a hash table).
For weighted graphs, we can use extra space at each node to store weight values.
If the chain of the adjacency list is too long, in order to improve the efficiency of the search, we can replace the chained list with other more efficient data structures, such as balanced binary search tree, etc. (e.g., red-black tree).
Pros and Cons
Pros:
- Space Efficiency: Requires
O(V + E)space, which is efficient for sparse graphs. - Flexibility: More flexible and better suited for graphs where the number of vertices is significantly higher than the number of edges.
Cons:
- Edge Look-Up: Checking if an edge exists between two vertices is
O(V)in the worst case, as it might involve traversing the entire list. - Implementation Complexity: Slightly more complex to implement compared to an adjacency matrix.
Reference:
- Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.