Home Linear Temporal Logic (LTL)
Post
Cancel

Linear Temporal Logic (LTL)

Posted Oct 8, 2023 Updated Oct 6, 2024
In (CS) Learning Note
8 min read

When it comes to reasoning about the behavior of systems over time, especially in the domain of formal verification, Linear Temporal Logic (LTL) stands out as a powerful tool.

Contents

Introduction to Linear Temporal Logic

What is Linear Temporal Logic?

Linear Temporal Logic (LTL) is a type of modal logic that allows for reasoning about propositions that may be true or false over time. Unlike classical logic, which focuses on the truth values of propositions at a single point in time, LTL considers the entire timeline of a system’s execution.

Linear Temporal Logic offers a robust framework for reasoning about system behaviors over time. Its ability to express intricate temporal properties makes it indispensable in the realm of formal verification, ensuring that systems operate reliably and as intended.

Syntax of LTL

LTL formulas are built from atomic propositions, Boolean operators, and temporal operators. Here are the primary components:

  • Atomic Propositions: These are basic propositions that can be either true or false.

  • Boolean Operators: Standard operators like AND (∧), OR (∨), NOT (¬).

  • Temporal Operators:

    • Globally (G): A property holds for all points in the future (It should contain the current point).
    • Finally (F): A property will eventually be true in the future (It can contain the current point).
    • Next (X): A property will be true at the next time step.
    • Until (U): A property holds until another becomes true.
    • All (A): A operator in LTL stands for “For All Paths”. When we use this operator, we are making a statement about all possible future paths that the system can take from a given state.

path: a path in a transition system is a finite or infinite sequence of states

Semantics of LTL

The semantics of LTL are defined over infinite sequences of states, called traces. Each LTL formula is evaluated over such traces:

  • Globally (G): If G p is true, then the proposition p holds at every point in the trace.

  • Finally (F): If F p is true, then the proposition p will be true at some point in the trace.

  • Next (X): If X p is true, then p will be true at the very next point in the trace.

  • Until (U): p U q means p holds continuously until q becomes true.

There is a special case for p U q:

If the first point is q, it always holds no matter what the following points are (Because q is first one, so, it doesn’t break “p holds continuously until q becomes true”). For example: S0(p)→S1(q), pathS0→S1 and pathS1 all hold for p U q.

  • All (A): A φmeans that “for all paths, φ holds”. In other words, no matter which path the system takes from the current state, the property φ will always be true.

LTL formulas are of two kinds:

  • path formulas:
    • tt, p : where p is an atomic proposition
    • if f and g are path formulas, then so are:
      • ¬f : not f
      • f ∧ g : f and g
      • X f : at the neXt point in time, f
      • F f : at some point in the Future, f
      • G f : Globally (at all future points) f
      • f U g : f Until g
  • state formulas:
    • A f : along All computation paths, f holds

Applications of LTL

LTL is widely used in the field of formal verification, especially in:

  • Model Checking: LTL formulas can specify properties that a system should satisfy. Model checkers then verify if a given system model adheres to these properties.

  • Runtime Verification: LTL can be used to monitor running systems and check if they adhere to specified properties in real-time.

  • Specification Writing: LTL provides a formal language to write precise requirements for systems, ensuring clarity and rigor.

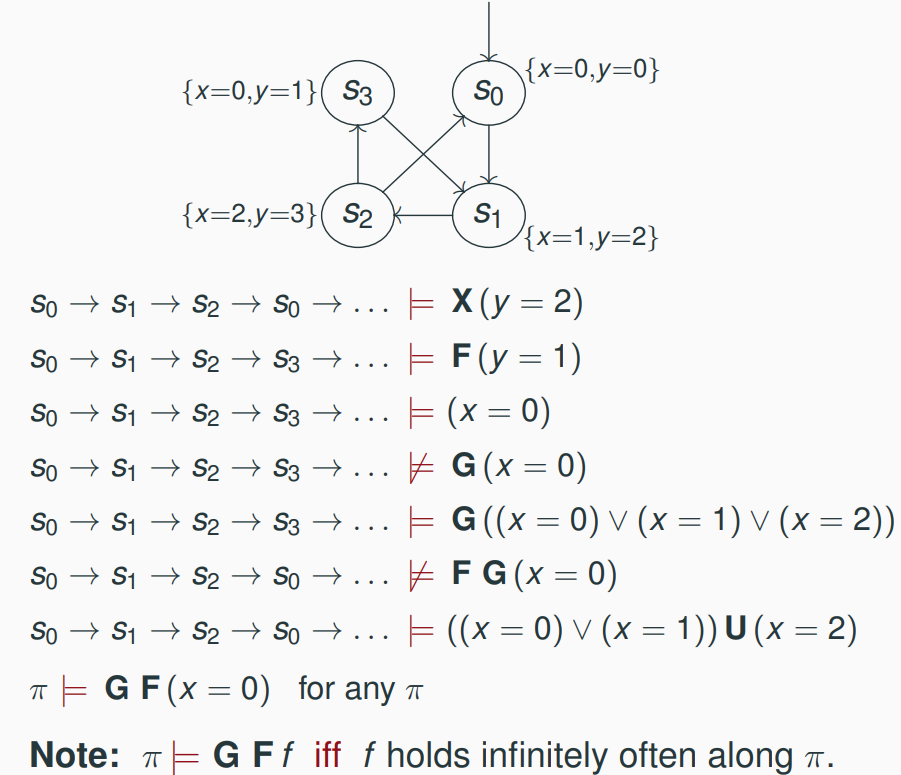
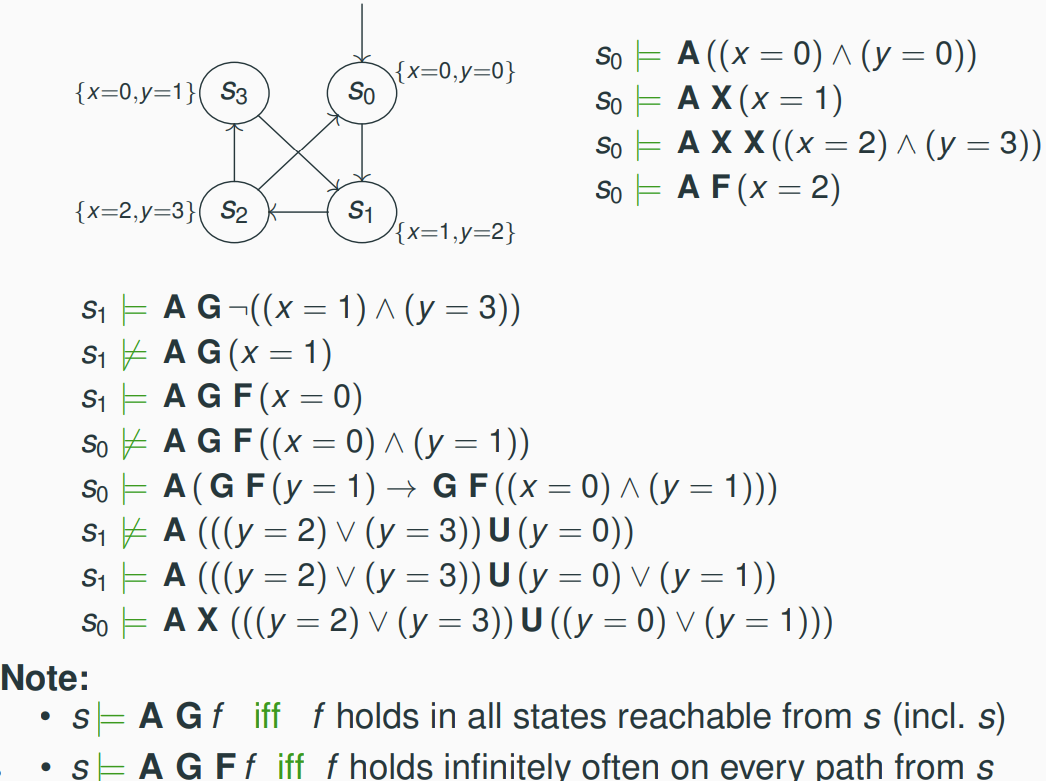
Some Examples about Semantics of LTL

Example 1

Example 2

Example 3 With Annotation

Semantics of LTL Matching Node Annotation
A F a holds in all states For all paths form all states, pass through S2(a) finally.
A F r holds in state S1 only Only all paths from state S1, pass through S1(r) finally. e.g. S3→S2→S4→S2→S4→…, doesn’t pass through S1(r)
A F g holds in states S1 and S3 Only all paths from states S1 and S3, pass through S3(g) finally. e.g. S2→S4→S2→S4→…, doesn’t pass through S3(g)
A G a holds in no state No path always stops at S2(a). So, it is clear that no state holds, because a is only in S2.
A G F a holds in all states For all paths, and for every point, pass through S2(a) finally.
A G F r holds in no state For all paths, there are some points, from them doesn’t pass through S1(r) finally. e.g. For path S1→S2. Then from S2, S2→S4→S2→S4→…, doesn’t pass through S1(r)
A (b U ¬b) holds in all states r,a,g all are ¬b, and after S4(b) always is S2(¬b). So, holds in all states
A (g U (a U r)) holds in state S1 only g U (a U r) equivalent to: g to a to r(ease of understanding, NOT rigorous). It seems like that there is no state holds because S2(a) can to S4(b), but S1 is r, so all paths from S1 hold for g U (a U r). Therefore, S1 holds A (g U (a U r))

Some LTL Patterns

  • invariance (always): A G p
    • “p remains invariantly true throughout every path”
  • guarantee (eventually): A F p
    • “p will eventually become true in every path”
  • stability (non-progress): A F G p
    • “there is a point in every path where p will become invariantly true”
  • recurrence (progress): A G F p
    • “if p happens to be false at any given point in a path, it is always guaranteed to become true again later”. Same as: “p holds infinitely often”
  • response: A G (p → F q)
    • “any state satisfying p is eventually followed by a state satisfying q”
  • precedence: A G (p → q U r)
    • “from any state satisfying p, the system will continuously satisfy property q until property r becomes true”
  • correlation: A ( F p → F q)
    • “if p holds at some point in the future, so does q”

Some Interesting Equivalences

¬ G p ≡ F ¬p

G p ≡ G G p

F p ≡ F F p

G (p ∧ q) ≡ G p ∧ G q

F (p ∨ q) ≡ F p ∨ F q

G F (p ∨ q) ≡ G F p ∨ G F q

p U q ≡ p U (p U q)

p U q ≡ (p U q) U q

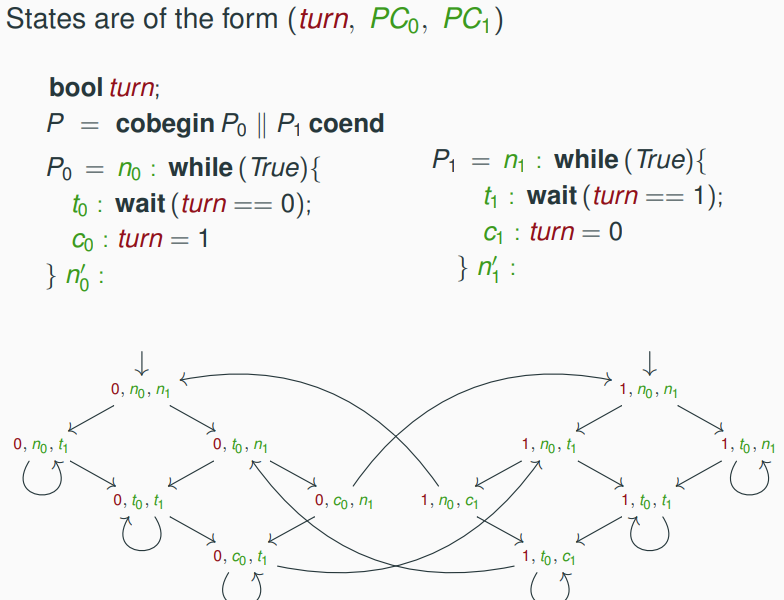
Application Example of Checking Mutual Exclusion

Temporal Properties for Mutual Exclusion

  • mutual exclusion: at most one process in critical section at any time (i.e. in every reachable state)
  • starvation freedom: whenever a process tries to enter its critical section, it will eventually succeed (along every computation path)
  • no strict sequencing: processes need not enter their critical section in strict sequence (i.e. there exists a computation path along which they don’t)

Mutual Exclusion: Checking Correctness

Atomic propositions:

  • c0 , c1 (critical state)
  • n0 , n1 (non-critical state)
  • t0 , t1 (trying to enter critical state)
  • mutual exclusion: at most one process in critical section at any time
    • A G ¬(c0 ∧ c1)
    • Need to check that ¬(c0 ∧ c1) is true at all states reachable from the initial states. (True)
  • absence of starvation: whenever a process tries to enter its critical section, it will eventually succeed
    • A G ((t0 → F c0) ∧ (t1 → F c1))
    • Need fairness assumptions for the property to hold. (False or True)
  • no strict sequencing: processes need not enter their critical section in strict sequence
    • can only express the negation of this property, but this is sufficient, since a counter-example to strict sequencing is proof for non-strict sequencing !
    • define Weak Until W operator: f W g = G f ∨ f U g
    • A ( G (c0 → c0 W (¬c0 ∧ ¬c0 W c1)) ∧ G (. . .) ) (False, So, no strict sequencing is True)

In the context of mutual exclusion, “no strict sequencing” refers to the principle that there is no predetermined or fixed order in which processes must be granted access to the critical section. In other words, a mutual exclusion solution should not enforce a strict order or sequence in which processes enter their critical sections.

(CS) Learning Note, Automated Software Verification
computer science software verification LTL Model Checking
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents
ip