Ideally, the insertion, deletion, and search operations of a binary search tree have a time complexity of O(log n). However, a binary search tree may degenerate into a linked list during frequent dynamic updates, and the time complexity becomes O(n).
To solve this complexity degradation problem, we need a balanced binary search tree, and the red-black tree is one of them. The red-black tree provides guaranteed O(log n) time complexity for basic operations such as search, insert, and delete.
- What is a Red-Black Tree?
- How to Prove the Red-Black Tree is “Approximately Balanced”?
- Applications of Red-Black Trees
What is a Red-Black Tree?
A red-black tree is a kind of self-balancing binary search tree where each node stores an extra bit for denoting the color of the node, either red or black. This color attribute ensures that the tree remains approximately balanced during insertions and deletions.
A red-black tree is a self-balancing binary search tree. However, the balanced nature of the red-black tree does not strictly adhere to the definition of a balanced binary tree (The height difference between the left and right subtree of each node is not more than 1).
Therefore, the red-black tree is often considered an approximately balanced binary search tree.
The red-black tree only achieves approximate balance, not strict balance. This is to ensure lower balance maintenance costs.
In contrast, AVL tree is a strictly balanced binary tree, so the search is very efficient. However, AVL trees have to pay more to maintain this high degree of balance. For AVL trees, it is more complicated and time-consuming to make adjustments for each insertion and deletion.
Properties of Red-Black Trees
Red-black trees must satisfy the following properties to maintain balance and ensure a height of O(log n), where n is the number of nodes:
- Color Property: Every node is either red or black.
- Root Property: The root is black.
- Leaf Property: Each leaf node must be black empty
NILnode (i.e., leaf nodes do not store data and are black). - Red Node Property: If a red node has children, both are black (i.e., no two red nodes can be adjacent).
- Black Depth Property: Every path from a node to its descendant leaf
NILnodes has the same number of black nodes.
These properties effectively control the tree’s height, maintaining balance and ensuring performance.
How to Prove the Red-Black Tree is “Approximately Balanced”?
- “Balanced” means that the performance of the binary tree does not degrade.
- “Approximately balanced” means that the performance of the binary tree does not degrade too much.
To prove that the red-black tree is “approximately balanced”:
- we only need to analyse whether the height of the red-black tree converges stably to
log n.
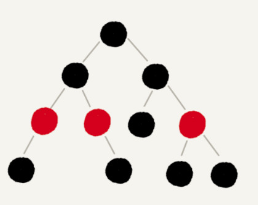
What happens if we remove the red node from the red-black tree?
From the above figure, we can see that each non-leaf node of the “black tree” (red node removed) has at least two children (this is not really absolute, as a red-black tree can have no red nodes. But in practice, this is almost negligible). Therefore, the height of the “black tree” (red node removed) not exceed log n.
What does the height become when we add the red node back in?
In a red-black tree, red nodes cannot be adjacent. So after adding the red node, the longest path will not exceed 2(log n), i.e. the height of the red-black tree is approximated 2(log n).
So, in the worst case, the height of the red-black tree is only just twice as large as the height of the highly balanced AVL tree (log n).
Applications of Red-Black Trees
- Databases: Red-black trees are used in database indices to speed up data retrieval.
- Associative Arrays: Languages like C++ and Java use red-black trees for ordered map implementations due to their performance guarantees.
- Priority Queues: With minor modifications, red-black trees can implement priority queues that support fast insertion and deletion of elements.
Reference:
- Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.