- Red-black tree is a good and bad data structure:
- “good” because of its stable and efficient performance.
- “bad” because of its implementation is challenging and complex.
The implementation of the red-black tree can be a bit difficult to understand. However, as developers, we don’t have to understand it completely (even if you understand it completely, you will forget it after a period of time). For most developers, it is not necessary to implement red-black trees during their work. The important thing is to understand the features and principles of red-black trees.
- Fundamental Principles of Red-Black Trees
- Critical Adjustment in Red-Black Tree
- Origin of the Red-Black Tree: The 2-3-4 Tree
- Implementing of Red-Black Tree
- Why Are the Leaf Nodes of the Red-Black Tree All Black
NILNodes?
Fundamental Principles of Red-Black Trees
Red-Black Trees balance the tree with every insert and delete operation, ensuring that the tree height remains logarithmic in relation to the number of nodes. This guarantees optimal worst-case time complexity for search, insert, and delete operations. The balance is maintained through the tree’s defining properties:
- Node Coloring: Every node is either red or black.
- Root and Leaf Properties: The root is always black, and all leaf nodes are black empty
NILnodes. - Red Node Rule: Red nodes cannot have red children (no two red nodes can be adjacent).
- Black Depth Rule: Every path from a given node to any of its descendant leaf nodes goes through the same number of black nodes.
By enforcing these rules, Red-Black Trees ensure that the longest path from the root to a leaf is no more than twice as long as the shortest path, which is what keeps the tree approximately balanced.
Critical Adjustment in Red-Black Tree
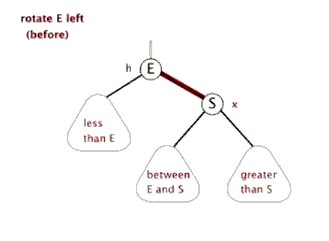
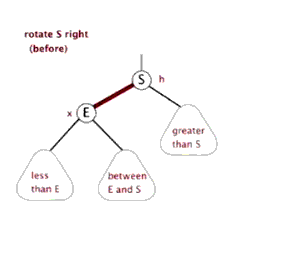
Rotation
Rotations are pivotal to maintaining the Red-Black Tree structure during insertions and deletions. They are used to shift pointers and change the parent-child relationships within the tree to preserve its balanced nature.
- Left Rotation: This operation is performed when the tree becomes too heavy on the right side. It involves rotating a node down and to the left to balance the tree. The right child of the node becomes the new parent of the rotated node.
rotate E left
- Right Rotation: This is the opposite of a left rotation and is performed when the tree is too heavy on the left side. The left child of a node becomes the new parent, and the original node is rotated down and to the right.
rotate S right
Rotations do not affect the black depth of nodes, which is crucial to maintain the properties of the Red-Black Tree.
Recoloring
Recoloring is turning a red node to black, or a black node to red.
Origin of the Red-Black Tree: The 2-3-4 Tree
What is a 2-3-4 Tree?
A 2-3-4 Tree, also known as a B-Tree of order 4, is a self-balancing tree where each node can have two, three, or four children, and correspondingly one, two, or three keys. The tree adjusts itself during insertions and deletions to maintain balance, ensuring that all leaf nodes are at the same depth.
a 2-3-4 Tree
Characteristics of 2-3-4 Trees
- Balance: Every leaf node is at the same distance from the root, which guarantees that operations are performed in logarithmic time.
- Multi-node Structure: Nodes can hold multiple keys and have multiple children, which is a distinguishing feature from binary trees.
- 2-node: node containing 1 element with 2 children;
- 3-node: node containing 2 elements with 3 children;
- 4-node: node containing 3 elements with 4 children;
- Adaptability: 2-3-4 Trees dynamically adjust their structure during operations to maintain balance without explicit tree rotations.
Transition to Red-Black Trees
While 2-3-4 Trees are powerful and efficient, their implementation can be complex due to the variability in the number of children and keys per node. Red-Black Trees were introduced as a binary-search-tree equivalent of 2-3-4 Trees, simplifying the structure while maintaining the same operational guarantees.
Red-Black Trees as Binary Models of 2-3-4 Trees
Red-Black Trees transform the multi-way branching of 2-3-4 Trees into binary branches through the use of two colors, red and black. The color coding in Red-Black Trees facilitates an equivalent to the 2-3-4 Tree’s balancing mechanics but with a simpler binary node structure.
Each node of a 2-3-4 tree corresponds to one structure of a red-black tree (using the red node).
- In Red-Black Trees, a red node with a black parent can be thought of as being merged with its parent.
nodes in 2-3-4 tree correspond to nodes in red-black tree
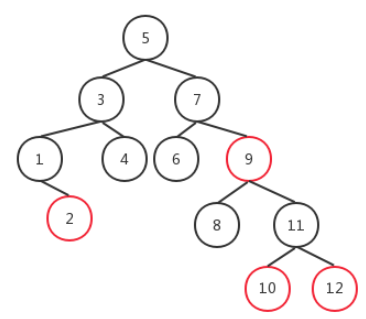converting the above 2-3-4 tree into a red-black tree (omit the black NIL leaf node)
Instead of splitting and merging nodes as in 2-3-4 Trees, Red-Black Trees use Rotation and Recoloring to maintain tree balance, effectively simulating the splitting and merging processes.
Implementing of Red-Black Tree
The process of adjusting the balance of the red-black tree is very similar to the process of restoring the Magic Cube:
- Don’t delve too deeply into this algorithm.
- You just need to understand that you can maintain the balance of the red-black tree as long as you follow a fixed set of steps and do not destroy its definition. It’s like restoring a Magic Cube:
- The process of restore has a fixed adjustment strategy. When you encounter a specific different situation, turn the corresponding few times. You just need to follow this restore step, and you will surely be able to restore the Magic Cube.
one of the adjustment strategies of restoring the Magic Cube
Just like the adjustment strategies of restoring the Magic Cube, there are different adjustment strategies when encountering different situations. The corresponding strategies are many and complex. The following only describes the general approach to adjustment.
Insertion
When a new node is inserted into a Red-Black Tree, it is initially colored red. This choice helps maintain the black depth property but may violate the red node rule if the parent node is also red. To fix potential violations, a series of steps is followed:
- Recoloring: If both the parent and uncle of a new node are red, changing both their colors to black (and the grandparent’s to red) can fix violations without rotations.
- Rotations: If recoloring isn’t enough, rotations are used to reshuffle the tree structure. Depending on the relative positions of the new node, its parent, and its grandparent, a combination of left and right rotations may be employed.
Deletion
Deletion in a Red-Black Tree can be complex because removing a black node may violate the black depth property. To restore the tree properties following a deletion:
- Replacement: If the deleted node had a red child, replacing the node with its child retains the properties. If the node was black and its child red, changing the child’s color to black rebalances the tree.
- Double Black Fix: If a black node is removed and leaves a “double black” hole, the tree must be adjusted using rotations and recolorings. This might involve complex cases where adjustments propagate up the tree.
Why Are the Leaf Nodes of the Red-Black Tree All Black NIL Nodes?
This is to make it easier to adjust the nodes to keep the tree balanced when inserting or deleting nodes.
When a new node is inserted into the tree or a node is deleted, it may create or remove leaf nodes. By ensuring that these leaf nodes are always black NIL nodes, we avoid introducing inconsistencies in the tree’s structure and properties.
To save space, when implementing a red-black tree, we can share a black NIL leaf node.
Reference:
- Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.
- https://www.cnblogs.com/crazymakercircle/p/16320430.html#autoid-h3-7-0-0
- https://www.cnblogs.com/zhenbianshu/p/8185345.html
