Skip lists are a fascinating and practical data structure that combines elements of both linked lists and balanced trees. Offering a clever probabilistic twist, skip lists provide efficient search, insertion, and deletion operations, comparable to those in balanced trees, but with a simpler implementation mechanism.
When we search using a skip list, each step reduces the search space by roughly half, which is like binary search.
- What is a Skip List?
- Java Implementation of a Skip List
- Time and Space Complexity of Skip Lists
- Why does Redis use skip lists instead of red-black trees for Sorted Sets?
What is a Skip List?
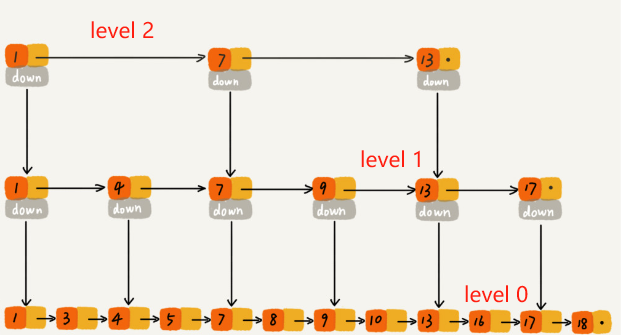
A skip list is a data structure that allows for fast search within an ordered sequence of elements. It achieves this by maintaining multiple layers of linked lists, each of which skips over fewer elements. The efficiency of skip lists comes from the ability to jump over large sections of the list, significantly reducing the number of steps to find an element.
A skip list consists of several layers of linked lists. The bottom layer is a simple linked list of all the elements. Each subsequent layer acts as an “express lane” over the previous list, containing fewer elements. Searching begins at the highest layer and moves down toward the bottom layer, making efficient jumps along the way.
Key Operations
- Search: Navigate through layers to quickly narrow down the interval containing the target.
- Insertion: Place the new element in the bottom list and selectively promote it to higher levels based on coin flips.
- Deletion: Similar to insertion, locate the item in each level and remove it.
Advantages of Skip Lists
- Simplicity: Easier to implement and understand compared to balanced trees like AVL or Red-Black trees.
- Efficient: Provides average time complexity of
O(log n)for search, insert, and delete operations. - Flexibility: Easily extended to allow for more advanced operations, such as range queries and non-uniform distributions.
Java Implementation of a Skip List
Implementing a skip list in Java involves creating node classes for each element in the list, where each node has pointers to its successors in various layers. Here’s a basic implementation:
This Java code demonstrates a simple skip list. The randomLevel method uses a probabilistic approach to determine the level of the new node.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
import java.util.Random;
class SkipListNode {
public int value;
public SkipListNode[] forward; // This will store the next node of each level. For example, forword[i] represents the next node of level i.
public SkipListNode(int level, int value) {
forward = new SkipListNode[level + 1]; // Initialize forward pointers array
this.value = value;
}
}
class SkipList {
private static final double P = 0.5; // Probability of each element being promoted to a higher level (levels are promoted at intervals of roughly 1/P nodes.)
private static final int MAX_LEVEL = 16;
private SkipListNode header;
private int level;
private Random random;
public SkipList() {
header = new SkipListNode(MAX_LEVEL, Integer.MIN_VALUE);
level = 0;
random = new Random();
}
public SkipListNode search(int value) {
SkipListNode current = header;
for (int i = level; i >= 0; i--) { // Searching from the top level
while (current.forward[i] != null && current.forward[i].value < value) {
current = current.forward[i]; // Move forward until reaching end or finding appropriate position
}
}
current = current.forward[0]; // Move to next node at bottom level
if (current != null && current.value == value) {
return current; // Return node if value found
} else {
return null; // Return null if value not found
}
}
public void insert(int value) {
SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];
SkipListNode current = header;
for (int i = level; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].value < value) {
current = current.forward[i];
}
update[i] = current;
}
current = current.forward[0];
if (current == null || current.value != value) {
int lvl = randomLevel();
if (lvl > level) {
for (int i = level + 1; i <= lvl; i++) {
update[i] = header;
}
level = lvl;
}
SkipListNode newNode = new SkipListNode(lvl, value);
for (int i = 0; i <= lvl; i++) {
newNode.forward[i] = update[i].forward[i];
update[i].forward[i] = newNode;
}
}
}
public void delete(int value) {
SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];
SkipListNode current = header;
for (int i = level; i >= 0; i--) {
while (current.forward[i] != null && current.forward[i].value < value) {
current = current.forward[i];
}
update[i] = current;
}
current = current.forward[0];
if (current != null && current.value == value) {
for (int i = 0; i <= level; i++) {
if (update[i].forward[i] != current) {
break;
}
update[i].forward[i] = current.forward[i];
}
while (level > 0 && header.forward[level] == null) {
level--;
}
}
}
// Generate random level (index layers to be created) for a new node
private int randomLevel() {
int lvl = 1;
while (random.nextDouble() < P && lvl < MAX_LEVEL) {
lvl++;
}
return lvl;
}
}
Time and Space Complexity of Skip Lists
Time Complexity
The time complexity for search, insert, and delete operations in a skip list primarily depends on the number of layers (or levels) and the number of elements in each layer. The average time complexity for these operations in a skip list is O(log n), where n is the number of elements in the list. Here’s a breakdown of how this is achieved:
- Search Operation:
- Starting from the topmost layer, the algorithm moves right until it finds an element greater than the target, then it moves down one layer.
- This process repeats until the target is found or the search concludes at the lowest layer.
- On average, each step reduces the search space by half (similar to Binary Search), leading to a logarithmic search time.
- Insert and Delete Operations:
- Similar to the search, insertions and deletions begin by finding the correct position using the search strategy.
- For insertions, nodes are probabilistically promoted to higher layers to maintain the skip list properties.
- Deletions require removal from all layers where the element appears, followed by possible re-adjustments.
- Both operations involve an initial search followed by modifications, maintaining the logarithmic time complexity on average.
- The key factor in calculating the time complexity of operations in a skip list is the height (maximum level) of the skip list.
- If the probability of each element being promoted to a higher level is
p(commonly 1/2), the expected height becomes log base1/pofn, which simplifies tolog₂ nwhenp = 1/2. - Each operation progresses vertically and horizontally within these bounds, contributing to the
log₂ ncomplexity. - The search count for each layer is constant, so it is omitted. Then we get time complexity:
O(log n)
- If the probability of each element being promoted to a higher level is
Space Complexity
- Space complexity of indexed nodes (the node not in level 0) is
O(n)- If the original linked list contains
nnodes:- the number of first level indexed nodes is
n/2, the number of second level indexed nodes isn/4, the number of third level indexed nodes isn/8and so on. - So, the sum of indexed nodes is:
n/2 + n/4 + n/8 + ... + 8 + 4 + 2 = n-2which isO(n).
- the number of first level indexed nodes is
- If the original linked list contains
- Overall space complexity is
O(n)Overall space complexity=Space complexity of indexed nodes+Space complexity of the original linked list- If the original linked list contains
nnodes, space complexity of the original linked list isO(n). - So, overall space complexity =
O(n) + O(n)=O(2n), which also isO(n)(omits constant).
- If the original linked list contains
Optimizing Space Usage
Although the space complexity of the skip list is O(n), it does take up more space than the original linked list. Therefore, we need to consider doing some optimisation.
To optimize the space usage in skip lists, consider limiting the maximum level or using dynamic strategies to adjust the level probabilities based on runtime metrics. This can help balance performance and space efficiency according to specific application needs.
Why does Redis use skip lists instead of red-black trees for Sorted Sets?
Red-black trees also allow for fast insertion, deletion, and search operations. Why does Redis choose to implement sorted sets using skip lists? Why not use red-black trees?
- The main reason is the core operations supported by sorted sets in Redis include searching for data in an interval (e.g., to search data between [100, 356].). For this operation, the red-black trees are not as efficient as skip lists
- Skip lists can locate the start of the range in
O(logn)time complexity, and then traversing through the original linked list sequentially. This is very efficient.
- Skip lists can locate the start of the range in
- Besides this, there are other reasons:
- Skip lists are simpler to implement in code than red-black trees. Simple means readable and less error-prone.
- Skip lists are more flexible. They can effectively balance execution efficiency and memory consumption by changing the index building strategy.
Reference:
- Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.