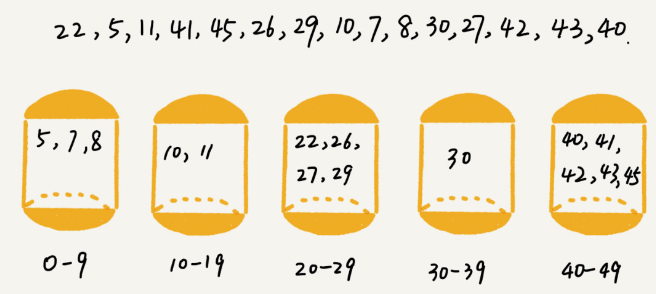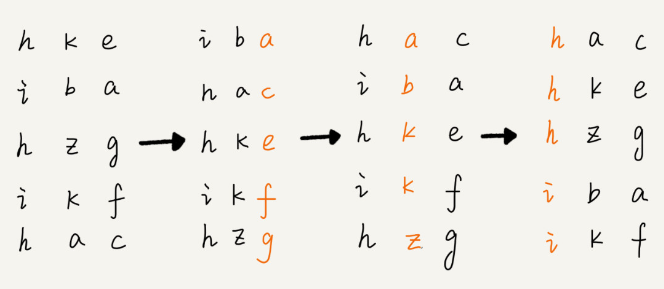Sorting Algorithms

Algorithm	Time Complexity (Average Case)	Best Time Complexity	Worst Time Complexity	Space Complexity	Is Stable	Is In-place
Bubble Sort	O(n^2)	O(n)	O(n^2)	O(1)	Yes	Yes
Direct Insertion Sort	O(n^2)	O(n)	O(n^2)	O(1)	Yes	Yes
Binary Insertion Sort	O(n^2)	O(n)	O(n^2)	O(1)	Yes	Yes
Selection Sort	O(n^2)	O(n^2)	O(n^2)	O(1)	No	Yes
Shell Sort	O(n^1.3)	O(n)	O(n^2)	O(1)	No	Yes
Merge Sort	O(n log n)	O(n log n)	O(n log n)	O(n)	Yes	No
Quick Sort	O(n log n)	O(n log n)	O(n^2)	O(log n)	No	Yes
Heap Sort	O(n log n)	O(n log n)	O(n log n)	O(1)	No	Yes
Bucket Sort	O(n log(n/m))	O(n)	O(n^2)	O(n)	Yes	No
Counting Sort	O(n + k)	O(n + k)	O(n + k)	O(k)	Yes	No
Radix Sort	O(nk)	O(nk)	O(nk)	O(n + k)	Yes	No

---

Contents

---

• Bubble Sort
• Insertion Sort
  • Direct Insertion Sort
  • Binary Insertion Sort
  • Shell Sort (Hill Sort)
• Selection Sort
• Merge Sort
• Quick Sort
• Heap Sort
• Linear Sort
  • Bucket Sort
  • Counting Sort
  • Radix Sort

---

Bubble Sort

Mechanism: Bubble Sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements, and swaps them if they are in the wrong order. The process is repeated until the list is sorted.

Advantages:

• Simple and easy to understand.
• Works well for small datasets or nearly sorted arrays.

Disadvantages:

• Inefficient for large datasets with a time complexity of O(n^2).

void bubbleSort(int arr[]) {
    int n = arr.length;
    for (int i = 0; i < n - 1; i++)
        for (int j = 0; j < n - i - 1; j++)
            if (arr[j] > arr[j + 1]) { // swap arr[j+1] and arr[j]
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
}

Insertion Sort

Direct Insertion Sort

Mechanism: This algorithm iteratively takes one element from the unsorted portion and finds its appropriate place in the sorted portion of the array.

Advantages:

• Simple implementation.
• Efficient for (nearly) sorted data sets.

Disadvantages:

• Poor efficiency on large, unsorted data sets.

void insertionSort(int array[]) {
    int n = array.length;
    for (int i = 1; i < n; ++i) {
        int key = array[i];
        int j = i - 1;

        while (j >= 0 && array[j] > key) {
            array[j + 1] = array[j];
            j = j - 1;
        }
        array[j + 1] = key;
    }
}

Why is insertion sort more popular than bubble sort since both bubble sort and insertion sort have the same time complexity O(n^2) and are stable sorting algorithms?

• Because data swapping in a bubbling sort is more complex than data movement in an insertion sort (bubbling requires 3 assignment operations, while insertion only requires 1)

Binary Insertion Sort

Mechanism: Similar to direct insertion but uses binary search to find the proper location for insertion, reducing comparisons.

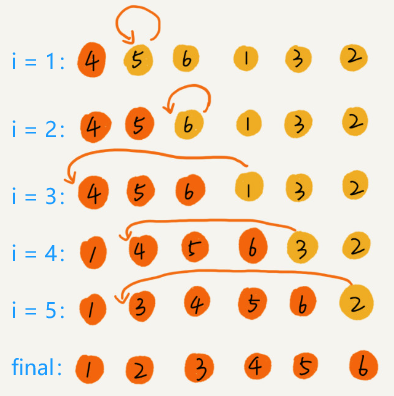same as the direct insertion sort (except that it’s faster to find the insertion position)

Advantages:

• Reduced number of comparisons.

Disadvantages:

• More complex than direct insertion sort.
• Movement of elements is still costly.

void binaryInsertionSort(int array[]) {
    for (int i = 1; i < array.length; i++) {
        int key = array[i];
        int insertedPosition = binarySearch(array, 0, i - 1, key);

        for (int j = i - 1; j >= insertedPosition; j--) {
            array[j + 1] = array[j];
        }
        array[insertedPosition] = key;
    }
}

int binarySearch(int array[], int start, int end, int key) {
    while (start <= end) {
        int mid = start + (end - start) / 2;
        if (key < array[mid]) {
            end = mid - 1;
        } else {
            start = mid + 1;
        }
    }
    return start;
}

Why is the time complexity of binary insertion sort still n2?

• Although the number of comparisons is reduced, the number of swaps is not, and all the elements still need to be shifted after the position is found.

Shell Sort (Hill Sort)

Mechanism: An extension of insertion sort that allows the exchange of far apart elements to improve speed. Shell sort improves the efficiency of insertion sort by moving larger elements in advance to reduce the number of reverse order pairs.

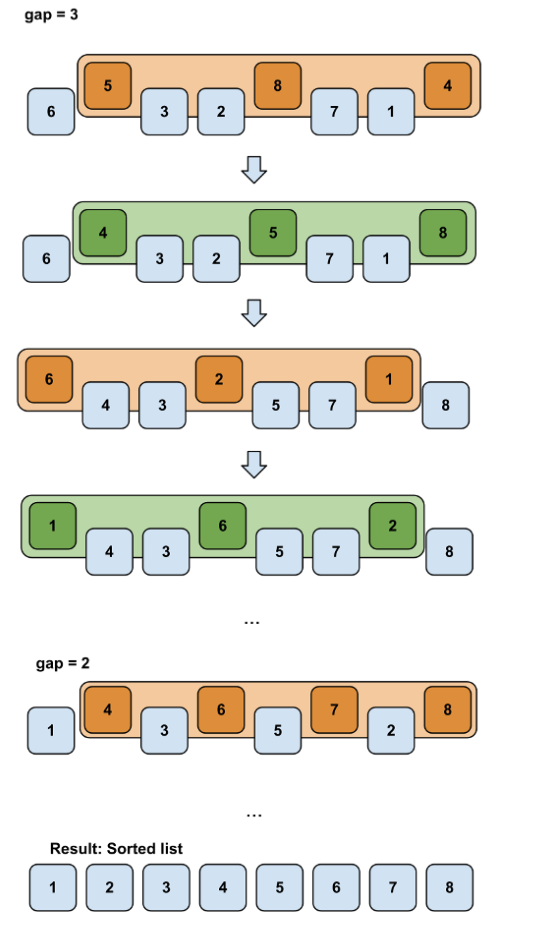from: http://stoimen.com/2012/02/27/computer-algorithms-shell-sort/

Advantages:

• Better handling of large data sets compared to simple insertion.

Disadvantages:

• Gap sequence choice is critical for performance.
  • Initially Shell proposed to take gap = n/2 and gap = gap/2 up to gap = 1. Later Knuth proposed to take gap = gap/3 + 1. Neither claim has been proved.

void shellSort(int array[]) {
    int n = array.length;
    for (int gap = n / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < n; i++) {
            int temp = array[i];
            int j = i;
            while (j - gap >= 0 && temp < arr[j - gap]) {
                arr[j] = arr[j - gap];
                j -= gap;
            }
            array[j] = temp;
        }
    }
}

Selection Sort

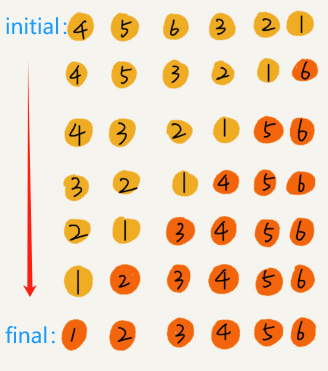
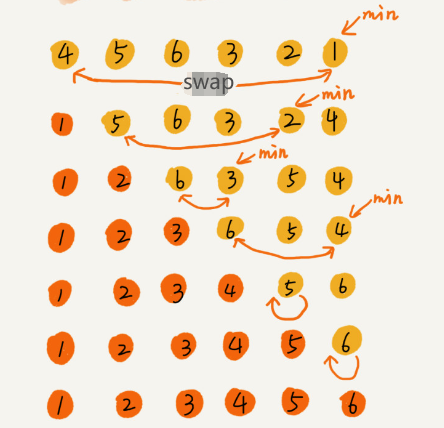
Mechanism: Repeatedly finding the minimum element (considering ascending order) from the unsorted part and putting it at the beginning.

Advantages:

• Simplicity and ease of understanding.

Disadvantages:

• Inefficient on large lists.

void selectionSort(int array[]) {
    int n = array.length;
    for (int i = 0; i < n-1; i++) {
        int min_idx = i;
        for (int j = i + 1; j < n; j++) {
            if (array[j] < array[min_idx]) {
                min_idx = j;
            }
        }

        int temp = array[min_idx];
        array[min_idx] = array[i];
        array[i] = temp;
    }
}

Is selection sort a stable sorting algorithm?

• No. Selection sort has to find the smallest of the remaining unsorted elements each time and swap places with the previous element, which breaks stability. For example, if you sort a set of 5, 8, 5, 2, 9 using the selection sort algorithm, the first time you find the smallest element, 2, and swap places with the first 5, the order of the first 5 and the middle 5 changes, so it is unstable.
  • It is for this reason that Selection Sort is slightly inferior to Bubble Sort and Insertion Sort.

Merge Sort

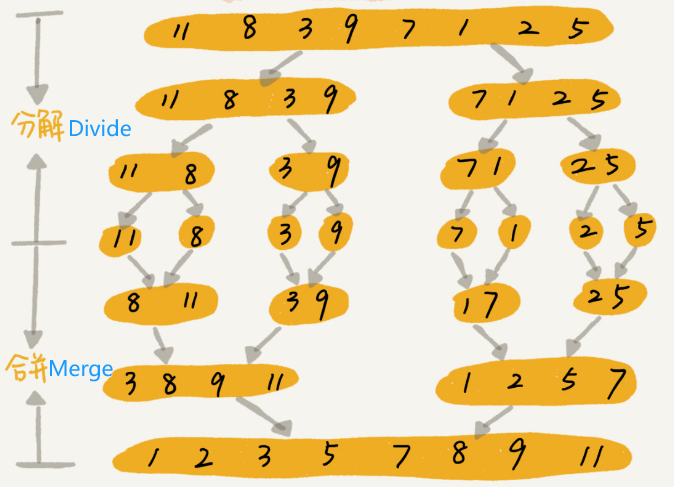
Mechanism: Merge Sort is a divide-and-conquer algorithm that divides the input array into two halves, calls itself for the two halves, and then merges the two sorted halves.

Advantages:

• Stable sorting algorithm.
• Consistently runs in O(n log n) time.

Disadvantages:

• Requires additional space proportional to the array size.
• Slightly more complex than other simple sorting algorithms.

void mergeSort(int[] arr) {
    if (arr == null || arr.length <= 1) {
        return;
    }
    mergeSort(arr, 0, arr.length - 1);
}

void mergeSort(int arr[], int l, int r) {
    if (l < r) {
        // Find the middle point
        int m = l + (r - l) / 2;

        // Sort first and second halves
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);

        // Merge the sorted halves
        merge(arr, l, m, r);
    }
}

// Function to merge the two haves arr[l..m] and arr[m+1..r] of array arr[]
void merge(int arr[], int left, int mid, int right) {
    int[] temp = new int[right - left + 1];

    int i = left;
    int j = mid + 1;
    int k = 0;

    while (i <= mid && j <= right) {
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else {
            temp[k++] = arr[j++];
        }
    }

    while (i <= mid) {
        temp[k++] = arr[i++];
    }

    while (j <= right) {
        temp[k++] = arr[j++];
    }

    for (int p = 0; p < temp.length; p++) {
        arr[left + p] = temp[p];
    }
}

Quick Sort

Mechanism: Quick Sort is a divide-and-conquer algorithm. It picks an element as a pivot and partitions the given array around the picked pivot. There are different versions of quickSort that pick pivot in different ways.

Advantages:

• One of the fastest sorting algorithms for average cases.
• Space-efficient and does not require additional storage.

Disadvantages:

• Worst-case time complexity can be O(n^2), although this is rare.
• Not stable, meaning it may change the relative order of elements with equal keys.

void quickSort(int[] arr) {
    if (arr == null || arr.length == 0) {
        return;
    }
    quickSort(arr, 0, arr.length - 1);
}

void quickSort(int arr[], int low, int high) {
    if (low < high) {
        /* pivotIndex is partitioning index, arr[pi] is now at right place */
        int pivotIndex = partition(arr, low, high);

        quickSort(arr, low, pivotIndex - 1);  // Before pi
        quickSort(arr, pivotIndex + 1, high); // After pi
    }
}

int partition(int arr[], int low, int high) {
    int pivot = arr[high];
    int i = (low - 1); // index of smaller element
    
    for (int j = low; j < high; j++) {
        if (arr[j] <= pivot) {
            i++;
            
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
    
    int temp = arr[i+1];
    arr[i+1] = arr[high];
    arr[high] = temp;

    return i+1;
}

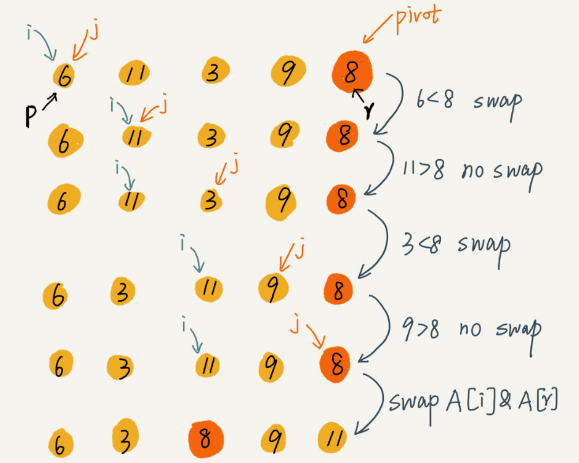partition(int arr[], int low, int high)

---

We can use partition() in the quick sort algorithm to find the K largest element in an unordered array in O(n) time complexity.

private static int quickSelect(int[] nums, int left, int right, int k) {
    if (left == right) {
        return nums[left];
    }

    int pivotIndex = partition(nums, left, right);

    if (k == pivotIndex) {
        return nums[k];
    } else if (k < pivotIndex) {
        return quickSelect(nums, left, pivotIndex - 1, k);
    } else {
        return quickSelect(nums, pivotIndex + 1, right, k);
    }
}

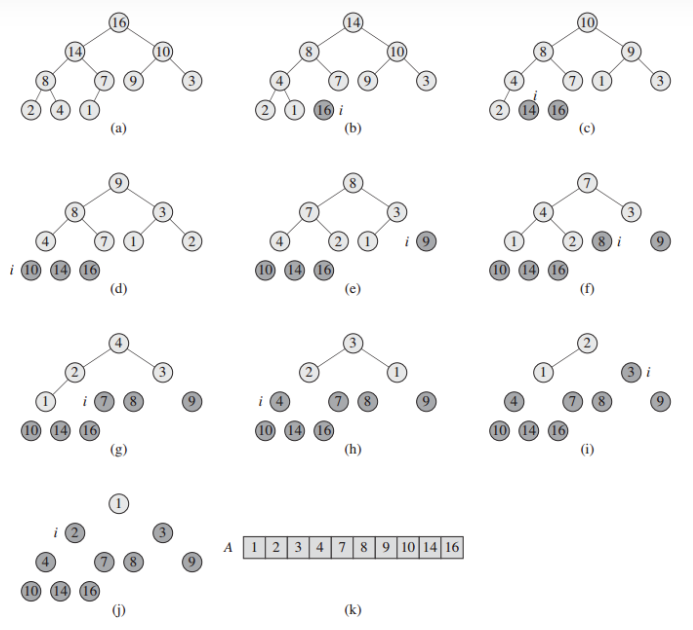
Heap Sort

Mechanism: Builds a max heap from the data, then repeatedly extracts the maximum element from the heap and rebuilds the heap until all elements are sorted.

Advantages:

• Good for large data sets, with consistent performance.

Disadvantages:

• Relatively complex algorithm, not stable.

void heapSort(int array[]) {
    int n = array.length;
    // Starting from the last non-leaf node (indexed n/2-1 ) and moving up to the root node (indexed 0 ), a heap operation (heapify) is performed on each node to construct a maximal heap
    for (int i = n / 2 - 1; i >= 0; i--) {
        heapify(array, n, i);
    }
   
    for (int i=n-1; i>0; i--) {
        int temp = array[0];
        array[0] = array[i];
        array[i] = temp;
        heapify(array, i, 0);
    }
}

void heapify(int array[], int n, int i) {
    int largest = i;
    int l = 2*i + 1;
    int r = 2*i + 2;
    if (l < n && array[l] > array[largest])
        largest = l;
    if (r < n && array[r] > array[largest])
        largest = r;
    if (largest != i) {
        int swap = array[i];
        array[i] = array[largest];
        array[largest] = swap;
        heapify(array, n, largest);
    }
}

In practice, why does Quick Sort perform better than Heap Sort?

1. Data access of Heap Sort is worse than Quick Sort.
   • For quick sort, data is accessed sequentially. Whereas, for heap sort, the data is accessed in jumps. This is not friendly to the CPU cache.
2. In general, Heap Sort has more data swaps than Quick Sort.

Linear Sort

Linear Sort refers to a sorting algorithm that has a linear time complexity (O(n), O(n + k), O(nk)).

Bucket Sort

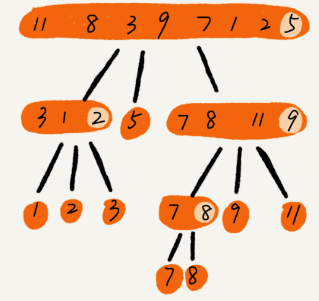
Mechanism: Distributes elements into several “buckets” and sorts these individually.

Advantages:

• Fast when the input is uniformly distributed.
• It Can be applied to external sorting.
  • External sorting means that the sorted data is stored in an external disk. (Due to the relatively large amount of data and limited memory, it is not possible to load all the data into internal memory)

Disadvantages:

• The requirements for the data to be sorted are very demanding (Ideally, the data is distributed evenly across the buckets).
• Performance depends on data distribution and bucket count.

public static void bucketSort(int[] arr, int bucketSize) {
    if (arr == null || arr.length <= 1) {
        return;
    }

    int minValue = arr[0];
    int maxValue = arr[0];
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] < minValue) {
            minValue = arr[i];
        } else if (arr[i] > maxValue) {
            maxValue = arr[i];
        }
    }

    int bucketCount = (maxValue - minValue) / bucketSize + 1;
    ArrayList<ArrayList<Integer>> buckets = new ArrayList<>(bucketCount);
    for (int i = 0; i < bucketCount; i++) {
        buckets.add(new ArrayList<>());
    }

    for (int i = 0; i < arr.length; i++) {
        int bucketIndex = (arr[i] - minValue) / bucketSize;
        buckets.get(bucketIndex).add(arr[i]);
    }

    int index = 0;
    for (int i = 0; i < bucketCount; i++) {
        Collections.sort(buckets.get(i));
        for (int j = 0; j < buckets.get(i).size(); j++) {
            arr[index++] = buckets.get(i).get(j);
        }
    }
}

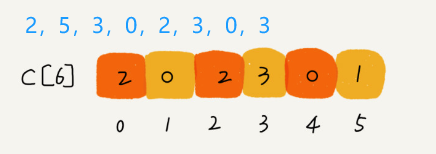
Counting Sort

Mechanism: Counts the occurrences of each value to sort. Counting sort is actually a special case of bucket sorting (Assign a bucket to each possible value so that the data values in each bucket are the same, eliminating the need to sort the buckets).

Advantages:

• Linear time complexity in the suitable context.

Disadvantages:

• Not suitable for data with large range relative to the number of elements.
• Not an in-place algorithm.

public static void countingSort(int[] arr) {
    // Assuming there are no negative numbers in arr
    int maxValue = arr[0];
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] > maxValue) {
            maxValue = arr[i];
        }
    }

    int[] count = new int[maxValue + 1];

    for (int num : arr) {
        count[num]++;
    }

    int index = 0;
    for (int i = 0; i <= maxValue; i++) {
        while (count[i] > 0) {
            arr[index++] = i;
            count[i]--;
        }
    }
}

Radix Sort

Mechanism: Sorts numbers digit by digit, starting from the least significant digit to the most significant.

Advantages:

• Can be faster than comparison-based algorithms for large data sets.

Disadvantages:

• Only works for integer keys or types that can be represented as such.
• Depends on another stable sort algorithm (like counting sort) for sorting digits.

public static void radixSort(int[] arr) {
    if (arr == null || arr.length <= 1) {
        return;
    }

    int maxVal = getMaxValue(arr);
    int exp = 1;

    while (maxVal / exp > 0) {
        countingSort(arr, exp);
        exp *= 10;
    }
}

private static int getMaxValue(int[] arr) {
    int maxVal = arr[0];
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] > maxVal) {
            maxVal = arr[i];
        }
    }
    return maxVal;
}

private static void countingSort(int[] arr, int exp) {
    int[] output = new int[arr.length];
    int[] count = new int[10];

    for (int i = 0; i < arr.length; i++) {
        count[(arr[i] / exp) % 10]++;
    }

    for (int i = 1; i < 10; i++) {
        count[i] += count[i - 1];
    }

    for (int i = arr.length - 1; i >= 0; i--) {
        output[count[(arr[i] / exp) % 10] - 1] = arr[i];
        count[(arr[i] / exp) % 10]--;
    }

    for (int i = 0; i < arr.length; i++) {
        arr[i] = output[i];
    }
}

---

Reference:

• Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.
• Stoimen et al. (2012) Stoimen’s web log. Available at: http://stoimen.com/2012/02/27/computer-algorithms-shell-sort/ (Accessed: 04 April 2024).