Linear lists, often simply referred to as lists, are the data structure that represents a sequence of elements arranged in a linear order. In addition to arrays and linked lists, stacks and queues are also important linear lists.
Introduction of Stacks and Queues
Stacks and queues are operation-constrained linear lists.
Why do we need operation-constrained linear lists (stacks and queues) since we have arrays and linked lists?
- Functionally, arrays or linked lists can indeed replace stacks and queues. However, arrays or linked lists expose too many operational interfaces, resulting in uncontrollable operations which are more prone to errors.
- This seems a lot like the idea of abstraction in OOP. We expose only the interfaces that should be exposed, and hide the complexity
Stack
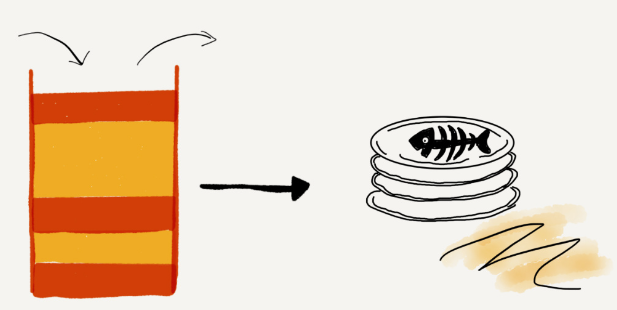
A stack is a linear data structure that follows the Last In, First Out (LIFO) principle. This means the last element added to the stack is the first one to be removed. You can think of a stack like a stack of plates; you can only add or remove the top plate.
A stack is like a pile of stacked plates. When we put the plates, we put them one by one from the bottom to the top; when we take them off, we take them one by one from the top to the bottom, and we can’t just pull them out of the middle.
Key Operations
- Push: Add an element to the top of the stack.
- Pop: Remove the element from the top of the stack.
- Peek: Return the top element without removing it from the stack.
Common Uses
- Expression Evaluation: Useful in evaluating and converting expressions (infix to postfix/prefix).
- Undo Mechanisms: Widely used in applications like text editors for implementing undo mechanisms.
- Depth-First Search (DFS): Essential in graph traversal algorithms like DFS for managing vertices to be explored.
- Function Call Management: Stacks are used in almost all modern programming languages to manage function calls and returns.
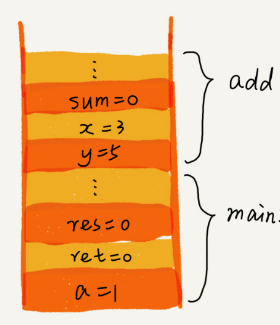
- Stacks are suitable for function call management due to their Last-In-First-Out (LIFO) property, which aligns well with the behaviour(nesting) of function calls and returns in programming languages. This mechanism ensures that the program flow returns to the correct location after each function call.
An Example of Function Call Management:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int main() {
int a = 1;
int ret = 0;
int res = 0;
ret = add(3, 5);
res = a + ret;
printf("%d", res);
reuturn 0;
}
int add(int x, int y) {
int sum = 0;
sum = x + y;
return sum;
}
Queue
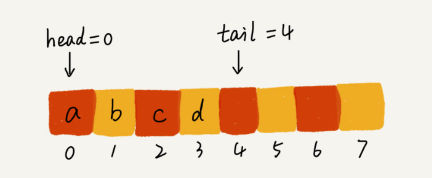
A queue is another linear data structure that operates on the First In, First Out (FIFO) principle. Elements are added at the rear and removed from the front, much like people waiting in line to get served at a store.
Key Operations
- Enqueue: Add an element to the end of the queue.
- Dequeue: Remove the element from the front of the queue.
- Peek/Front: Look at the front element without removing it.
Common Uses
- Job Scheduling: Queues are fundamental in scenarios where tasks need to be managed and executed in an orderly fashion, such as printing jobs.
- Buffering: Used for managing data streams in networking, where data packets are buffered in queues for processing.
- Breadth-First Search (BFS): Essential in graph traversal algorithms like BFS for managing vertices to be explored.
Implementing Stacks and Queues
While stacks and queues can be implemented using arrays or linked lists, each method has its pros and cons:
- Array-Based Implementation: Easy to implement but has a fixed size, which can be limiting.
- LinkedList-Based Implementation: Offers dynamic sizing but requires more memory due to storage of additional pointers.
Implementation of Stack
Using an Array
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class ArrayStack {
private int[] stack; // Array used to store the elements of the stack
private int top; // Index of the top element in the stack
private int capacity; // Maximum capacity of the stack
// Constructor to initialize the stack
public ArrayStack(int size) {
capacity = size;
stack = new int[capacity];
top = -1; // Initialize top to -1 indicating the stack is empty
}
// Method to add an element to the top of the stack
public void push(int value) {
if (top == capacity - 1) {
throw new RuntimeException("Stack Overflow"); // Check for stack overflow
}
stack[++top] = value; // Place value at the next available position and increment top
}
// Method to remove and return the top element of the stack
public int pop() {
if (isEmpty()) {
throw new RuntimeException("Stack Underflow"); // Check for stack underflow
}
return stack[top--]; // Return the top element and decrement top
}
// Method to return the top element without removing it
public int peek() {
if (isEmpty()) {
throw new RuntimeException("Stack Underflow"); // Check if the stack is empty
}
return stack[top]; // Return the top element
}
// Method to check if the stack is empty
public boolean isEmpty() {
return top == -1; // Return true if top is -1, indicating stack is empty
}
// Method to get the size of the stack
public int size() {
return top + 1; // Size is the index of the top element + 1
}
}
Using a Linked List
- With LinkedList, capacity is no longer limited (but extra memory is used to store pointers).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class LinkedListStack {
private ListNode top; // Top of the stack
// Constructor initializes the stack to be empty
public LinkedListStack() {
this.top = null;
}
// Method to add an element to the top of the stack
public void push(int value) {
ListNode newNode = new ListNode(value); // Create a new node with the given value
newNode.next = top; // Link the new node to the previous top
top = newNode; // Update the top to the new node
}
// Method to remove and return the top element of the stack
public int pop() {
if (isEmpty()) {
throw new RuntimeException("Stack is empty"); // Check if the stack is empty
}
int result = top.value; // Get the top element
top = top.next; // Move the top to the next element
return result; // Return the top element
}
// Method to return the top element without removing it
public int peek() {
if (isEmpty()) {
throw new RuntimeException("Stack is empty"); // Check if the stack is empty
}
return top.value; // Return the value of the top element
}
// Method to check if the stack is empty
public boolean isEmpty() {
return top == null; // Return true if top is null
}
}
Using two Queues
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class StackUsingTwoQueues {
private Queue<Integer> queue1; // Primary queue to store elements
private Queue<Integer> queue2; // Secondary queue used for the push operation
// Constructor initializes two empty queues
public StackUsingTwoQueues() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
// Method to push an element onto the stack
public void push(int x) {
// Always insert the new element into the empty queue (queue2)
queue2.add(x);
// Move all elements from queue1 to queue2, preserving the LIFO order
while (!queue1.isEmpty()) {
queue2.add(queue1.remove());
}
// Swap the roles of the two queues
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
// Method to remove the top element of the stack and return it
public int pop() {
if (queue1.isEmpty()) {
throw new RuntimeException("Stack is empty");
}
return queue1.remove(); // Remove the element from the front of queue1
}
// Method to get the top element of the stack without removing it
public int top() {
if (queue1.isEmpty()) {
throw new RuntimeException("Stack is empty");
}
return queue1.peek(); // Retrieve the element from the front of queue1 without removing it
}
// Method to check if the stack is empty
public boolean empty() {
return queue1.isEmpty(); // Check if queue1 is empty
}
}
Implementation of Queue
- The implementation of a queue is slightly more complex than the implementation of a stack
- Because implementing a queue requires caring for two things: front and rear.
- Whereas implementing a stack only requires caring for one thing: top.
Using an Array
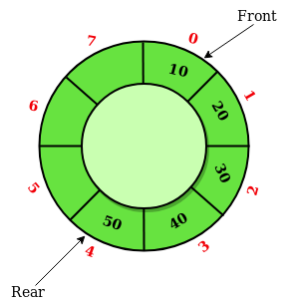
- The following code implements what is actually a circular queue
- Circular queue efficiently utilises memory by reusing freed-up space when elements are dequeued
- Using a circular queue eliminates the movement of elements in the array when writing code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class ArrayQueue {
private int[] queue; // Array to hold the elements of the queue
private int front; // Index of the front element
private int rear; // Index where the next element will be inserted
private int size; // Current number of elements in the queue
private int capacity; // Maximum capacity of the queue
// Constructor to initialize the queue
public ArrayQueue(int capacity) {
this.capacity = capacity;
this.queue = new int[capacity];
this.front = 0;
this.rear = -1;
this.size = 0;
}
// Method to add an element to the rear of the queue
public void enqueue(int value) {
if (isFull()) {
throw new RuntimeException("Queue is full");
}
rear = (rear + 1) % capacity; // Move rear to the next position in a circular manner
queue[rear] = value; // Insert the new element at the rear
size++; // Increase the size of the queue
}
// Method to remove and return the front element of the queue
public int dequeue() {
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
int result = queue[front]; // Retrieve the front element
front = (front + 1) % capacity; // Move front to the next position in a circular manner
size--; // Decrease the size of the queue
return result;
}
// Method to return the front element without removing it
public int peek() {
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
return queue[front];
}
// Method to check if the queue is empty
public boolean isEmpty() {
return size == 0;
}
// Method to check if the queue is full
public boolean isFull() {
return size == capacity;
}
}
Using a Linked List
- With LinkedList, capacity is no longer limited (but extra memory is used to store pointers).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class LinkedListQueue {
private Node front; // Pointer to the front of the queue
private Node rear; // Pointer to the rear of the queue
private int size; // Number of elements in the queue
// Constructor initializes an empty queue
public LinkedListQueue() {
this.front = null;
this.rear = null;
this.size = 0;
}
// Method to add an element to the rear of the queue
public void enqueue(int data) {
Node newNode = new Node(data);
if (rear == null) {
// If the queue is empty, both front and rear are the new node
front = rear = newNode;
} else {
// Add the new node at the end of the queue and change rear
rear.next = newNode;
rear = newNode;
}
size++; // Increment the size of the queue
}
// Method to remove and return the front element of the queue
public int dequeue() {
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
int data = front.data; // Retrieve the data at the front
front = front.next; // Move front to the next node
if (front == null) {
rear = null; // If the queue becomes empty, rear must also be null
}
size--; // Decrement the size of the queue
return data;
}
// Method to check if the queue is empty
public boolean isEmpty() {
return front == null;
}
// Method to get the front element of the queue
public int peek() {
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
return front.data;
}
// Method to get the size of the queue
public int size() {
return size;
}
}
Using two Stacks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class QueueUsingTwoStacks {
private Stack<Integer> stackIn; // Stack to handle enqueue operations
private Stack<Integer> stackOut; // Stack to handle dequeue operations
// Constructor initializes two stacks
public QueueUsingTwoStacks() {
stackIn = new Stack<>();
stackOut = new Stack<>();
}
// Method to add an element to the rear of the queue
public void enqueue(int x) {
stackIn.push(x); // Push element to the 'stackIn'
}
// Method to remove and return the front element of the queue
public int dequeue() {
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
moveStackInToStackOut(); // Ensure 'stackOut' has the current elements
return stackOut.pop(); // Pop the element from 'stackOut'
}
// Method to return the front element without removing it
public int peek() {
if (isEmpty()) {
throw new RuntimeException("Queue is empty");
}
moveStackInToStackOut(); // Ensure 'stackOut' has the current elements
return stackOut.peek(); // Peek the element from 'stackOut'
}
// Method to check if the queue is empty
public boolean isEmpty() {
return stackIn.isEmpty() && stackOut.isEmpty();
}
// Helper method to transfer elements from 'stackIn' to 'stackOut'
private void moveStackInToStackOut() {
if (stackOut.isEmpty()) { // Only transfer if 'stackOut' is empty
while (!stackIn.isEmpty()) {
stackOut.push(stackIn.pop()); // Transfer all elements from 'stackIn' to 'stackOut'
}
}
}
}
Reference:
- Wang, Zheng (2019) The Beauty of Data Structures and Algorithms. Geek Time.