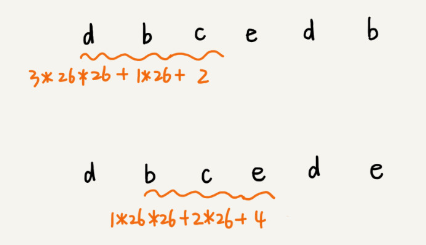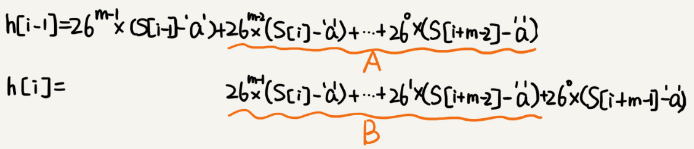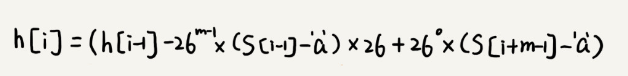Relatively Simple String Matching Algorithms: BF and RK

String matching is a fundamental problem in computer science, where the goal is to find occurrences of a pattern within a text. This problem is crucial in various applications, including text search, DNA sequencing, and plagiarism detection.

Contents

String Matching Problem
- Definitions
Brute Force (BF) String Matching
Rabin-Karp (RK) String Matching

String Matching Problem

Given a text T and a pattern P, the string matching problem involves finding all occurrences of P in T. Both T and P consist of characters from a finite alphabet set.

Definitions

Text (T): The main string in which we search for the pattern.
Pattern (P): The substring we are looking for within the text.

Brute Force (BF) String Matching

Introduction

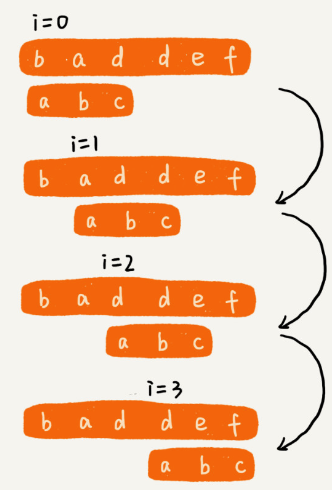
The Brute Force algorithm is the simplest method for string matching. It checks for the pattern at every possible position in the text until a match is found or all positions are exhausted.

How Brute Force Works

Alignment: Align the pattern P with the beginning of the text T.
Comparison: Compare each character of P with the corresponding character in T.
Shift: If a mismatch occurs, shift the pattern one position to the right and repeat the comparison.
Repeat: Continue this process until the pattern is found or the text is exhausted.

Example Implementation

Here’s a simple implementation of the Brute Force algorithm in Python:

        
      
// Returns the index of the first occurrence
public static int bruteForce(String text, String pattern) {
    int n = text.length();
    int m = pattern.length();

    for (int i = 0; i <= n - m; i++) {
        int j = 0;
        while (j < m && text.charAt(i + j) == pattern.charAt(j)) {
            j++;
        }
        if (j == m) {
            return i;  // Pattern found at index i
        }
    }
    return -1;  // Pattern not found
}

Pros and Cons of Brute Force

Pros:

Simplicity: Easy to understand and implement.
No Preprocessing: Requires no preprocessing of the text or pattern.

Cons:

Inefficiency: Time complexity is O(n*m) in the worst case, making it impractical for large texts and patterns.
Redundant Comparisons: Compares characters multiple times, leading to inefficiency.

The BF algorithm has a high time complexity of O(n*m), but in practice it is a relatively common string matching algorithm. There are two reasons for this:

In practice, the performance of the BF algorithm is not as bad as expected.

For most cases, the length of the pattern string and the main string are not too long.

And, although the theoretical worst-case time complexity is O(n*m), in most cases the algorithm performs much more efficiently than that (it doesn’t need to compare all m characters).

The BF algorithm is simple and the code implementation is also very simple.

Simplicity means that it is not error-prone, and if there are bugs, they are easy to exposed and fixed.

In engineering, simplicity is preferred under the premise of meeting performance requirements.

Rabin-Karp (RK) String Matching

Introduction

The full name of the RK algorithm is the Rabin-Karp algorithm, named after its inventors, Rabin and Karp. The Rabin-Karp algorithm uses hashing to achieve more efficient string matching. Instead of checking each position individually, it calculates a hash value for the pattern and compares it with hash values of substrings of the text.

How Rabin-Karp Works

Hash Calculation: Compute the hash value of the pattern P and the first substring of T of length m.
Comparison: Compare the hash value of P with the hash value of the current substring. If they match, compare the actual characters to confirm the match.
Rolling Hash: Use a rolling hash technique to compute the hash value of the next substring efficiently.
Repeat: Continue this process until the pattern is found or the text is exhausted.

Hash Calculation

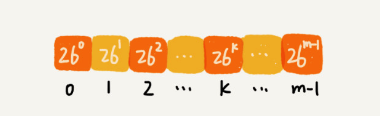
For hash calculation, we assume that the character set of the string to be matched contains only K characters, and we can represent a substring by a Base-K number, which is converted into a decimal number and used as the hash value of the substring.

For example, if the string we want to process contains only the 26 lowercase letters from a to z, then we represent a string in Base-26 number. We map the 26 characters from a to z to the 26 numbers from 0 to 25, where a is 0, b is 1, and so on, and z is 25.

hash calculation

This hash algorithm has a feature that the formula for calculating the hash values of two neighbouring substrings in the main string is related. As shown in the following figure:

Two neighbouring substrings, s[i-1] and s[i], have an intersection of the corresponding computation formulas. In other words, we can use the hash value of s[i-1] to calculate the s[i] quickly.

Example Implementation

Here’s a simple implementation of the Rabin-Karp algorithm in Python:

        
      
// if the string we want to process contains only the 26 lowercase letters from `a` to `z`
private static final int PRIME = 26;

public static int rabinKarp(String text, String pattern) {
    int m = pattern.length();
    int n = text.length();
    if (m > n) {
        return -1;
    }

    long patternHash = createHash(pattern, m);
    long textHash = createHash(text, m);

    for (int i = 0; i <= n - m; i++) {
        if (patternHash == textHash) {
            return i;
        }
        if (i < n - m) {
            textHash = recalculateHash(text, i, i + m, textHash, m);
        }
    }

    return -1;
}

// Method to calculate hash value of a string
private static long createHash(String str, int m) {
    long hash = 0;
    for (int i = 0; i < m; i++) {
        hash += (str.charAt(i) - 'a') * Math.pow(PRIME, m - i - 1);
    }
    return hash;
}

// Method to recalculate hash value when sliding the window
private static long recalculateHash(String str, int oldIndex, int newIndex, long oldHash, int m) {
    long newHash = oldHash - (str.charAt(oldIndex) - 'a') * (long)Math.pow(PRIME, m - 1);
    newHash = (newHash * PRIME + (str.charAt(newIndex) - 'a'));
    return newHash;
}

Note: In the above code implementation, we use long to store the hash value. If the pattern is too long, it may cause the hash value to exceed the range of long (-9,223,372,036,854,775,808 to 9,223,372,036,854,775,807), and then the algorithm will fail.

The calculation of 26^(m-1) can be improved by searching the array. We calculate 26^0, 26^1, 26^2……26^(m-1) in advance, and store them in an array of length m. In this way, we only need to search for the corresponding numbers according to the index, eliminating the need for repetitive calculations.

For this algorithm, you may be worried about hash conflicts (i.e. different strings may correspond to the same hash value). In fact, the hash algorithm described above does not have hash conflicts. That means that a string corresponds to a base-26 number, and different strings must have different hash values. This may not be very intuitive, but you can think of it in analogy with decimal.

However, sometimes hash conflicts are allowed in order to simplify the hash algorithm, or to control the hash value in a certain data range. For example, we can add the numbers corresponding to each letter in the string. And the final sum is used as the hash value. This hash algorithm produces a hash value with a relatively much smaller range of data. But, how should we handle hash conflicts?

In fact, the solution is quite simple. When we find that two string hashes are equal, we just need to compare the strings themselves again. But then, the worst time complexity degrades to O(n*m). However, in general, there will not be many conflicts, and the RK algorithm is still more efficient than the BF algorithm.

Pros and Cons of Rabin-Karp

Pros:

Efficiency: Time complexity is O(n).
Hashing: Efficiently handles large texts using hashing.

Cons:

Spurious Hits: Hash collisions may lead to spurious hits, requiring additional character comparisons.
Hash Calculation Overhead: Computing and managing hash values can add complexity and overhead.