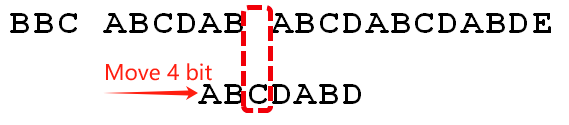Common String Matching Algorithms: KMP

String matching is a common problem in computer science, where the goal is to find occurrences of a pattern within a text. The Knuth-Morris-Pratt (KMP) algorithm is one of the most efficient solutions for this problem, providing linear-time complexity.

Contents

What is KMP Algorithm?
How KMP Works
Implementation in Java

What is KMP Algorithm?

The Knuth-Morris-Pratt (KMP) algorithm, named after its inventors Donald Knuth, Vaughan Pratt, and James H. Morris, efficiently searches for a pattern within a text by preprocessing the pattern to determine how it should shift upon a mismatch. This preprocessing step enables the algorithm to avoid unnecessary comparisons, achieving a time complexity of O(n + m), where n is the length of the text and m is the length of the pattern.

The Basic Idea of the KMP

The fundamental idea behind the KMP algorithm is to avoid unnecessary comparisons by utilising the information gathered from previous matches. Unlike the brute force approach, which rechecks characters that have already been matched, KMP uses a preprocessing step to remember where to continue from when a mismatch occurs.

Advantages of KMP

Efficiency: KMP provides a linear-time solution to the string matching problem, making it significantly faster than the brute force approach, especially for large texts.
No Backtracking: The algorithm eliminates the need for backtracking in the text, improving performance and predictability.
Predictable Performance: KMP guarantees a worst-case time complexity of O(n + m), making it reliable for various applications.

Disadvantages of KMP

Memory Usage: KMP requires additional space (O(m)) for the LPS array. For very large patterns, this can be significant. Although this is usually not a major issue, in memory-constrained environments, this can be a drawback.
Complex Preprocessing: The preprocessing step of computing the LPS (Longest Proper Suffix) array requires additional time and space. Although this is linear, it can be relatively complex to implement and understand compared to simpler algorithms like BF.

How KMP Works

The KMP algorithm is relatively complex. Before understanding how it works, it is important to understand the following concepts:

Prefix: Prefixes of a string are all the substrings that start at the start of the string.
- For example, the prefixes of the string ABCD include: A, AB, ABC.
Suffix: Suffixes of a string are all the substrings that end at the end of the string.
- For example, the suffixes of the string ABCD include: D, CD, BCD.
Prefix Function (Failure Function): The core of the KMP algorithm is the computation of the prefix function (also known as the “failure function”), which is used to compute the longest proper suffix (LPS).
Longest Proper Suffix (LPS): LPS is an array, which helps determine how much to shift the pattern in case of a mismatch.

Step 1: Preprocessing the Pattern (Compute LPS)

The first step of the KMP algorithm involves preprocessing the pattern to compute the LPS array. This array helps determine how much the pattern should shift upon encountering a mismatch.

But what exactly is LPS array? And how is it computed?
- Specifically, for each position i of the pattern string P, LPS[i] indicates the longest length of both prefix and suffix in the substring of the P before i. (This sentence may be difficult to understand. But let me give you an example so that you can easily understand it.)

Assume we want to compute the LPS of this pattern string: ABCDABD:

The result (LPS) is [0, 0, 0, 0, 1, 2]. And the specific process of computation is shown below:

All Prefixes of Pattern	Index	Prefixes of the Prefix	Suffixes of the Prefix	both prefix and suffix	the longest length
A	0	-	-	-	0
AB	1	A	B	-	0
ABC	2	A, AB	BC, C	-	0
ABCD	3	A, AB, ABC	BCD, CD, D	-	0
ABCDA	4	A, AB, ABC, ABCD	BCDA, CDA, DA, A	A	1
ABCDAB	5	A, AB, ABC, ABCD, ABCDA	BCDAB, CDAB, DAB, AB, B	AB	2

Step 2: Searching the Text

With the LPS array, we can easily implement the KMP algorithm and avoid unnecessary comparisons:
- If the currently matched characters are the same, continue comparing the next characters.
- If the currently matched characters are different, according to the value in the LPS array, move the pattern string to the right by an appropriate distance.
  - Assuming that the current number of matching characters is q: Number of shifted bits = q - LPS[q - 1]

For example:

q = 6
LPS[5] = 2
Number of shifted bits = 6 - 2 = 4

Repeat the above process until it ends.

Implementation in Java

Here’s a simple implementation of the KMP algorithm in Java:

        
      
public static int KMPSearch(String text, String pattern) {
    int n = text.length();
    int m = pattern.length();
    if (m > n) {
        return -1;
    }

    int[] lps = prefixFunction(pattern);
    int q = 0;

    for (int i = 0; i < n; i++) {
        while (q > 0 && pattern.charAt(q) != text.charAt(i)) {
            q = lps[q - 1];
        }
        if (pattern.charAt(q) == text.charAt(i)) {
            q++;
        }
        if (q == m) {
            return i - m + 1;
        }
    }
    return -1;
}

private static int[] prefixFunction(String pattern) {
    int m = pattern.length();
    int[] lps = new int[m - 1];
    int k = 0;

    for (int q = 1; q < m - 1; q++) {
        while (k > 0 && pattern.charAt(k) != pattern.charAt(q)) {
            k = lps[k - 1];
        }
        if (pattern.charAt(k) == pattern.charAt(q)) {
            k++;
        }
        lps[q] = k;
    }

    return lps;
}